- Description
- Calculation Variations
- Input
- Options
- Availability
- Related Keywords
- Examples
- ReadAnharm Input
- ReadFCHT Input
Description
This calculation-type keyword computes force constants and the resulting vibrational frequencies. Intensities are also computed. By default, the force constants are determined analytically if possible, by single numerical differentiation for methods for which only first derivatives are available, and by double numerical differentiation for those methods for which only energies are available.
Vibrational frequencies are computed by determining the second derivatives of the energy with respect to the Cartesian nuclear coordinates and then transforming to mass-weighted coordinates. This transformation is only valid at a stationary point. Thus, it is meaningless to compute frequencies at any geometry other than a stationary point for the method used for frequency determination.
For example, computing 6-311G(d) frequencies at a 6-31G(d) optimized geometry produces meaningless results. It is also incorrect to compute frequencies for a correlated method using frozen core at a structure optimized with all electrons correlated, or vice-versa. The recommended practice is to compute frequencies following a previous geometry optimization using the same method. This may be accomplished automatically by specifying both Opt and Freq within the route section for a job.
Note also that the CPHF (coupled perturbed SCF) method used in determining analytic frequencies is not physically meaningful if a lower energy wavefunction of the same spin multiplicity exists. Use the Stable keyword to test the stability of Hartree-Fock and DFT wavefunctions.
Calculation Variations
Additional related properties may also be computed during frequency calculations, including the following:
- When frequencies are done analytically, polarizabilities are also computed automatically; when numerical differentiation is required (or requested with Freq=Numer), polarizabilities must be explicitly requested using the Polar keyword (e.g., CCSD Freq Polar).
- The VCD option may be used to compute the vibrational circular dichroism (VCD) intensities in addition to the normal frequency analysis at the Hartree-Fock and DFT levels [Cheeseman96a].
- The ROA option computes analytic Raman optical activity intensities [Helgaker94, Dukor00, Ruud02a, Barron04, Thorvaldsen08, Cheeseman11a]. However, see Polar=ROA for the recommended method and model chemistries for predicting ROA spectra.
- Pre-resonance Raman intensities may be computed by specifying one of the Raman options, and also including CPHF=RdFreq within the route and specifying the desired frequency in the input file (see the examples for additional information).
- Frequency-dependent polarizabilities and hyperpolarizabilities may be computed by including CPHF=RdFreq within the route (subject to their usual availability restrictions).
- Vibrational-rotational coupling can be computed using Freq=VibRot [Califano76, Miller80, Papousek82, Clabo88, Page88, Adamo90, Miller90, Page90, Cossi03].
- The Anharmonic option performs numerical differentiation to compute anharmonic frequencies and zero-point energies [Califano76, Miller80, Papousek82, Clabo88, Page88, Miller90, Page90, Barone04, Barone05] and anharmonic vibrational-rotational couplings [Adamo90, Barone94, Minichino94, Barone95, Cossi03, Bloino12] (as requested). This option is only available for methods with analytic second derivatives: Hartree-Fock, DFT, CIS and MP2. Full anharmonic IR intensities are computed [Bloino12, Bloino15a]. The DCPT2 [Kuhler96, Bloino12a] and HDCPT2 [Bloino12a] methods support resonance-free computations of anharmonic frequencies and partition functions. Anharmonic VCD and ROA spectra can also be predicted [Bloino15]. Calculations in solution are supported [Cappelli11].
- There are several options for performing an analysis for an electronic excitation using the Franck-Condon [Sharp64, Doktorov77, Kupka86, Zhixing89, Berger97, Peluso97, Berger98, Borrelli03, Weber03, Coutsias04, Dierksen04, Lami04, Dierksen04a, Dierksen05, Liang05, Jankowiak07, Santoro07, Santoro07a, Santoro08, Barone09, Bloino10, Baiardi13], Herzberg-Teller method [Herzberg33, Sharp64, Small71, Orlandi73, Lin74, Santoro08, Barone09, Bloino10, Baiardi13] or combined Franck-Condon/Herzberg-Teller [Santoro08, Barone09, Bloino10, Baiardi13] methods (see the Options and additional input sections). They can be used to predict vibronic spectra and intensities, as well as resonance Raman spectra [Egidi14, Baiardi14]. Vibronic computations support chiral spectroscopies as well (ECD and CPL) [Barone12, Barone14]. For a tutorial review, see [Bloino16].
The keyword Opt=CalcAll requests that analytic second derivatives be done at every point in a geometry optimization. Once the requested optimization has completed all the information necessary for a frequency analysis is available. Therefore, the frequency analysis is performed and the results of the calculation are archived as a frequency job.
Input
The SelectNormalModes and SelectAnharmonicModes options require additional input. The modes to select are specified in a separate blank-line terminated input section. The initial mode list is always empty.
Integers and integer ranges without a keyword are interpreted as mode numbers (e.g., 1 5-9); these can also be preceded by not in order to exclude rather than include the specified atoms (e.g., not 10-20).
The keywords atoms and notatoms can be used to define an atom list whose modes should be included/excluded (respectively). Atoms can also be specified by ONIOM layer via the [not]layer keywords, which accept these values: real for the real system, model for the model system in a 2-layer ONIOM, middle for the middle layer in a 3-layer ONIOM, and small for the model layer of a 3-layer ONIOM. Atoms may be similarly included/excluded by residue with residue and notresidue, which accept lists of residue names or numbers. Both keyword sets function as shorthand forms for atom lists.
Here are some examples:
| 2-5 | Includes modes 2 through 5. |
| atoms=O | Includes modes involving oxygen atoms. |
| 1-20 atoms=Fe | Includes modes 1 through 20 and any modes involving iron atoms. |
| layer=real notatoms=H | Includes modes for heavy atoms in low layer (subject to default threshold). |
Options
Retrieving Force Constants
ReadFC
Requests that the force constants from a previous frequency calculation be read from the checkpoint file, and the mode and thermochemical analysis be repeated, presumably using a different temperature, pressure, or isotopes, at minimal computational cost. Note that since the basis set is read from the checkpoint file, no general basis should be input. If the Raman option was specified in the previous job, then do not specify it again when using this option.
Requesting Specific Spectra
Raman
Compute Raman intensities in addition to IR intensities. This is the default for Hartree-Fock. It may be specified for DFT and MP2 calculations. For MP2, Raman intensities are produced by numerical differentiation of dipole derivatives with respect to the electric field. (Raman is equivalent to NRaman for this method.)
NRaman
Compute polarizability derivatives by numerically differentiating the analytic dipole derivatives with respect to an electric field. This is the default for MP2 if Freq=Raman.
NNRaman
Compute polarizability derivatives by numerically differentiating the analytic polarizability with respect to nuclear coordinates.
NoRaman
Skips the extra steps required to compute the Raman intensities during Hartree-Fock analytic frequency calculations, saving 10-30% in CPU time.
VCD
Compute the vibrational circular dichroism (VCD) intensities in addition to the normal frequency analysis. This option is valid for Hartree-Fock and DFT methods. This option also computes optical rotations (see Polar=OptRot).
ROA
Compute dynamic analytic Raman optical activity intensities using GIAOs [Cheeseman11a]. This procedure requires one or more incident light frequencies to be supplied in the input to be used in the electromagnetic perturbations (CPHF=RdFreq is the default with Freq=ROA). This option is valid for Hartree-Fock and DFT methods. Note that the Polar=ROA keyword is often a better choice. NNROA says to use the numerical ROA method from Gaussian 03; this is useful only for reproducing the results of prior calculations.
Anharmonic Frequency Analysis
Anharmonic
Do numerical differentiation along modes to compute zero-point energies, anharmonic frequencies, and anharmonic vibrational-rotational couplings if VibRot is also specified. This option is only available for methods with analytic second derivatives: Hartree-Fock, DFT, CIS, and MP2.
ReadAnharm
Read an input section with additional parameters for the vibrational-rotational coupling and/or anharmonic vibrational analysis (VibRot or Anharmonic options). Available input options are listed in the “Availability” tab.
ReadHarmonic
Read the central point force constants and normal modes from a previous harmonic frequency calculation and avoid repeating the calculation at the central point.
ReadDifferentharmonic
Read the central point energy, forces, and force constants from a previous calculation and then compute 3rd and 4th derivatives at the current (presumably lower) level of theory for anharmonic spectra.
SelectAnharmonicModes
Read an input section selecting which modes are used for differentiation in anharmonic analysis. The format of this input section is discussed in the “Input” tab. SelAnharmonicModes is a synonym for this option.
Vibronic Spectra: Franck-Condon, Herzberg-Teller and FCHT
The following options perform an analysis for an electronic excitation using the corresponding method; these jobs use vibrational analysis calculations for the ground state and the excited state to compute the amplitudes for electronic transitions between the two states. The vibrational information for the ground state is taken from the current job (Freq or Freq=ReadFC), and the vibrational information for the excited state is taken from a checkpoint file, whose name is provided in a separate input section (enclose the path in quotes if it contains internal spaces). The latter will be from a CI-Singles or TD-DFT Freq=SaveNormalModes calculation.
The ReadFCHT option can be added to cause additional input to be read to control these calculations (see the “Availability” tab), and the SelFCModes option can be used to select the modes involved. In the latter case, the excited state checkpoint file would typically have been generated with Freq=(SelectNormalModes, SaveNormalModes) with the same modes selected.
FranckCondon
Use the Franck-Condon method [Sharp64, Doktorov77, Kupka86, Zhixing89, Berger97, Peluso97, Berger98, Borrelli03, Weber03, Coutsias04, Dierksen04, Lami04, Dierksen04a, Dierksen05, Liang05, Jankowiak07, Santoro07, Santoro07a, Barone09] (the implementation is described in [Santoro07, Santoro07a, Santoro08, Barone09]). FC is a synonym for this option. Transitions for ionizations can be analyzed instead of excitations. In this case, the molecule specification corresponds to the neutral form, and the additional checkpoint file named in the input section corresponds to the cation.
HerzbergTeller
Use the Herzberg-Teller method [Herzberg33, Sharp64, Small71, Orlandi73, Lin74, Santoro08] (the implementation is described in [Santoro08]). HT is a synonym for this option.
FCHT
Use the Franck-Condon-Herzberg-Teller method [Santoro08].
Emission
Indicates that emission rather than absorption should be simulated for a Franck-Condon and/or Herzberg-Teller analysis. In this case, within the computation, the initial state is the excited state, and the final state is the ground state (current job=ground state, second checkpoint file=excited state). This option allows you to specify alternatives to the default temperature, pressure, frequency scale factor the sources of frequency data for the ground and excited state are as described previously.
ReadFCHT
Read an input section containing parameters for the calculation. Available input options are documented in the “Availability” tab. This input section precedes that for ReadAnharmon if both are present.
Other Calculation Variations and Properties
VibRot
Analyze vibrational-rotational coupling.
Projected
For a point on a mass-weighted reaction path (IRC), compute the projected frequencies for vibrations perpendicular to the path. For the projection, the gradient is used to compute the tangent to the path. Note that this computation is very sensitive to the accuracy of the structure and the path [Baboul97]. Accordingly, the geometry should be specified to at least 5 significant digits. This computation is not meaningful at a minimum.
TProjected
Perform a projected harmonic frequency analysis if the RMS force is ≥ 1.d-3 Hartree/Bohr and perform regular harmonic analysis if the RMS force is smaller.
HinderedRotor
Requests the identification of internal rotation modes during the harmonic vibrational analysis [McClurg97, Ayala98, McClurg99]. If any modes are identified as internal rotation, hindered or free, the thermodynamic functions are corrected. The identification of the rotating groups is made possible by the use of redundant internal coordinates. Because some structures, such as transition states, may have a specific bonding pattern not automatically recognized, the set of redundant internal coordinates may need to be altered via the Geom=Modify keyword. Rotations involving metals require additional input via the ReadHinderedRotor option (see below).
If the force constants are available on a previously generated checkpoint file, additional vibrational/internal rotation analyses may be performed by specifying Freq=(ReadFC, HinderedRotor). Since Opt=CalcAll automatically performs a vibrational analysis on the optimized structure, Opt=(CalcAll, HinderedRotor) may also be used.
ReadHinderedRotor
Causes an additional input section to be read containing the rotational barrier cutoff height (in kcal/mol) and optionally the periodicity, symmetry number and multiplicity for rotational modes. Rotations with barrier heights larger than the cutoff value will be automatically frozen. If the periodicity value is negative, then the corresponding rotor is also frozen. You must provide the periodicity, symmetry and spin multiplicity for all rotatable bonds contain metals. The input section is terminated with a blank line, and has the following format:
| VMax-value | |
| Atom1 Atom2 periodicity symmetry spin | Repeated as necessary. |
| … |
Normal Modes
HPModes
Include the high precision format (to five figures) vibrational frequency eigenvectors in the frequency output in addition to the normal three-figure output.
InternalModes
Print modes as displacements in redundant internal coordinates. IntModes is a synonym for this option.
SaveNormalModes
Save all modes in the checkpoint file. SaveNM is a synonym for this option. It is the default.
ReadNormalModes
Read saved modes from the checkpoint file. ReadNM is a synonym for this option. NoReadNormalModes, or NoReadNM, is the default.
SelectNormalModes
Read input selecting the particular modes to display. SelectNM is a synonym for this option. NoSelectNormalModes, or NoSelectNM, is the default. AllModes says to include all modes in the output. The format of this input section is discussed in the “Input” tab. Note that this option does not affect the functioning of SaveNormalModes, which always saves all modes in the checkpoint file.
SortModes
Sort modes by ONIOM layer in the output.
ModelModes
Display only modes involving the smallest model system in an ONIOM calculation.
MiddleModes
Display only modes involving the two model systems in a 3-layer ONIOM.
PrintDerivatives
Print normal mode derivatives of the dipole moment, polarizability, and so on.
PrintFrozenAtoms
By default, the zero displacements for frozen atoms are not printed in the mode output. This option requests that all atoms be listed.
NoPrintNM
Used to suppress printing of the normal mode components during a frequency calculation. The frequencies and intensities are still reported for each mode.
Geometry-Related Options
ModRedundant
Read-in modifications to redundant internal coordinates (i.e., for use with InternalModes). Note that the same coordinates are used for both optimization and mode analysis in an Opt Freq, for which this is the same as Opt=ModRedundant. See the discussion of the Opt keyword for details on the input format.
ReadIsotopes
This option allows you to specify alternatives to the default temperature, pressure, frequency scale factor and/or isotopes—298.15 K, 1 atmosphere, no scaling, and the most abundant isotopes (respectively). It is useful when you want to rerun an analysis using different parameters from the data in a checkpoint file.
Be aware, however, that all of these can be specified in the route section (Temperature, Pressure and Scale keywords) and molecule specification (the Iso parameter), as in this example:
#T Method/6-31G(d) JobType Temperature=300.0 … … 0 1 C(Iso=13) …
ReadIsotopes input has the following format:
| temp pressure [scale] | Values must be real numbers. |
| isotope mass for atom 1 | |
| isotope mass for atom 2 | |
| … | |
| isotope mass for atom n |
Where temp, pressure, and scale are the desired temperature, pressure, and an optional scale factor for frequency data when used for thermochemical analysis (the default is unscaled). The remaining lines hold the isotope masses for the various atoms in the molecule, arranged in the same order as they appeared in the molecule specification section. If integers are used to specify the atomic masses, the program will automatically use the corresponding actual exact isotopic mass (e.g., 18 specifies 18O, and Gaussian uses the value 17.99916).
Algorithm Variations and Execution Options
Analytic
This specifies that the second derivatives of the energy are to be computed analytically. This option is available only for RHF, UHF, CIS, CASSCF, MP2, and all DFT methods, and it is the default for those cases.
Numerical
This requests that the second derivatives of the energy are to be computed numerically using analytically calculated first derivatives. It can be used with any method for which gradients are available and is the default for those for which gradients but not second derivatives are available. Freq=Numer can be combined with Polar=Numer in one job step.
FourPoint
Do four displacements instead of two for each degree of freedom during numerical frequencies, polarizabilities, or Freq=Anharm. This gives better accuracy and less sensitivity to step size at the cost of doing twice as many calculations.
DoubleNumer
This requests double numerical differentiation of energies to produce force constants. It is the default and only choice for those methods for which no analytic derivatives are available. EnOnly is a synonym for DoubleNumer.
Cubic
Requests numerical differentiation of analytic second derivatives to produce third derivatives. Applicable only to methods having analytic frequencies but no analytic third derivatives.
Step=N
Specifies the step-size for numerical differentiation to be 0.0001*N (in Angstoms unless Units=Bohr has been specified). If Freq=Numer and Polar=Numer are combined, N also specifies the step-size in the electric field. The default is 0.001 Å for Hartree-Fock and correlated Freq=Numer, 0.005 Å for GVB and CASSCF Freq=Numer, and 0.01 Å for Freq=EnOnly. For Freq=Anharmonic or Freq=VibRot, the default is 0.025 Å.
Restart
This option restarts a frequency calculation after the last completed geometry. A failed frequency job may be restarted from its checkpoint file by simply repeating the route section of the original job, adding the Restart option to the Freq=Numer keyword/option. No other input is required.
Analytic frequencies can be restarted with the Restart keyword provided that the read-write file was named and saved from the failed job. See the description of that keyword for more information and an example.
DiagFull
Diagonalize the full (3Natoms)2 force constant matrix—including the translation and rotational degrees of freedom—and report the lowest frequencies to test the numerical stability of the frequency calculation. This precedes the normal frequency analysis where these modes are projected out. Its output reports the lowest 9 modes, the upper 3 of which correspond to the 3 smallest modes in the regular frequency analysis. Under ideal conditions, the lowest 6 modes reported by this analysis will be very small in magnitude. When they are significantly non-zero, it indicates that the calculation is not perfectly converged/numerically stable. This may indicate that translations and rotations are important modes for this system, that a better integration grid is needed, that the geometry is not converged, etc. The system should be studied further in order to obtain accurate frequencies. See the “Examples” tab for the output from this option. DiagFull is the default; NoDiagFull says to skip this analysis.
TwoPoint
When computing numerical derivatives, make two displacements in each coordinate. This is the default. FourPoint will make four displacements but only works with Link 106 (Freq=Numer). Not valid with Freq=DoubleNumer.
NFreq=N
Requests that the lowest N frequencies be solved for using Davidson diagonalization. At present, this option is only available for ONIOM(QM:MM) model chemistries.
WorkerPerturbations
During numerical frequencies using Linda parallelism, run separate displacements on each worker instead of parallelizing each energy+derivative evaluation across the cluster. This strategy is more efficient, but it requires specifying an extra worker on the master node. It is the default if at least 3 Linda workers were specified. NoWorkerPerturbations suppresses this behavior.
Availability
Analytic frequencies are available for the AM1, PM3, PM3MM, PM6, PDDG, DFTB, DFTBA, HF, DFT, MP2, CIS, TD and CASSCF methods.
Numerical frequencies are available for MP3, MP4(SDQ), CID, CISD, CCD, CCSD, EOM-CCSD and QCISD.
Raman is available for the HF, DFT and MP2 methods.
VCD and ROA are available for HF and DFT methods.
Anharmonic is available for HF, DFT, MP2 and CIS methods.
Freq and NMR can both be on the same route for HF and DFT.
Examples
Frequency Output. The basic components of the output from a frequency calculation are discussed in detail in chapter 4 of Exploring Chemistry with Electronic Structure Methods [Foresman15].
New Gaussian users are often surprised to see frequency calculation output that looks like that of a geometry optimization:
GradGradGradGradGradGradGradGradGradGradGradGradGradGradGrad Berny optimization. Initialization pass.
Link 103, which performs geometry optimizations, is executed at the beginning and end of all frequency calculations. This is done so that the quadratic optimization step can be computed using the correct second derivatives. Occasionally an optimization will complete according to the normal criterion using the approximate Hessian matrix, but the step size is actually larger than the convergence criterion when the correct second derivatives are used. The next step is printed at the end of a frequency calculation so that such problems can be identified. If you think this concern is applicable, use Opt=CalcAll instead of Freq in the route section of the job, which will complete the optimization if the geometry is determined not to have fully converged (usually, given the full second derivative matrix near a stationary point, only one additional optimization step is needed), and will automatically perform a frequency analysis at the final structure.
Specifying #P in the route section produces some additional output for frequency calculations. Of most importance are the polarizability and hyperpolarizability tensors (the latter in Raman calculations only); although, they still may be found in the archive entry in normal print-level jobs. They are presented in lower triangular and lower tetrahedral order, respectively (i.e., αxx, αxy, αyy, αxz, αyz, αzz and βxxx, βxxy, βxyy, βyyy, βxxz, βxyz, βyyz, βxzz, βyzz, βzzz), in the standard orientation:
Dipole = 2.37312183D-16 -6.66133815D-16 -9.39281319D-01
Polarizability= 7.83427191D-01 1.60008472D-15 6.80285860D+00
-3.11369582D-17 2.72397709D-16 3.62729494D+00
HyperPolar = 3.08796953D-16 -6.27350412D-14 4.17080415D-16
5.55019858D-14 -7.26773439D-01 -1.09052038D-14
-2.07727337D+01 4.49920497D-16 -1.40402516D-13
-1.10991697D+01
#P also produces a bar-graph of the simulated spectra for small cases.
Thermochemistry analysis follows the frequency and normal mode data:
Zero-point correction= .023261 (Hartree/Particle) Thermal correction to Energy= .026094 Thermal correction to Enthalpy= .027038 Thermal correction to Gibbs Free Energy= .052698 Sum of electronic and zero-point Energies= -527.492585 E0=Eelec+ZPE Sum of electronic and thermal Energies= -527.489751 E= E0+ Evib+ Erot+Etrans Sum of electronic and thermal Enthalpies= -527.488807 H=E+RT Sum of electronic and thermal Free Energies= -527.463147 G=H-TS
The raw zero-point energy correction and the thermal corrections to the total energy, enthalpy, and Gibbs free energy (all of which include the zero-point energy) are listed, followed by the corresponding corrected energy. The analysis uses the standard expressions for an ideal gas in the canonical ensemble. Details can be found in McQuarrie [McQuarrie73] and other standard statistical mechanics texts. In the output, the various quantities are labeled as follows:
| E (Thermal) | Contributions to the thermal energy correction |
| CV | Constant volume molar heat capacity |
| S | Entropy |
| Q | Partition function |
The thermochemistry analysis treats all modes other than the free rotations and translations as harmonic vibrations. For molecules having hindered internal rotations, this can produce slight errors in the energy and heat capacity at room temperatures and can have a significant effect on the entropy. The contributions of any very low frequency vibrational modes are listed separately so that their harmonic contributions can be subtracted from the totals and their correctly computed contributions included should they be group rotations and high accuracy is required. Expressions for hindered rotational contributions to these terms can be found in Benson [Benson68]. The partition functions are also computed, with both the bottom of the vibrational well and the lowest (zero-point) vibrational state as reference.
Pre-resonance Raman. This calculation type is requested with one of the Raman options in combination with CPHF=RdFreq. The frequency specified for the latter should be chosen as follows:
- Determine the difference in frequency between the peak of interest in the UV/visible absorption spectrum and the incident light used in the Raman experiment.
- Perform a TD calculation using a DFT method in order to determine the predicted location of the same peak.
- Specify a frequency for CPHF=RdFreq which is shifted from the predicted peak by the same amount as the incident light differs from the observed peak.
Pre-resonance Raman results are reported as additional rows within the normal frequency tables:
Harmonic frequencies (cm**-1), IR intensities (KM/Mole), Raman
scattering activities (A**4/AMU), depolarization ratios for plane
and unpolarized incident light, reduced masses (AMU), force constants
(mDyne/A), and normal coordinates:
1
B1
Frequencies -- 1315.8011
Red. masses -- 1.3435
Frc consts -- 1.3704
IR Inten -- 7.6649
Raman Activ -- 0.0260
Depolar (P) -- 0.7500
Depolar (U) -- 0.8571
RamAct Fr= 1-- 0.0260 Additional output lines begin here.
Dep-P Fr= 1-- 0.7500
Dep-U Fr= 1-- 0.8571
RamAct Fr= 2-- 0.0023
Dep-P Fr= 2-- 0.7500
Dep-U Fr= 2-- 0.8571
Vibration-Rotation Coupling Output. If the VibRot option is specified, then the harmonic vibrational-rotational analysis appears immediately after the normal thermochemistry analysis in the output, introduced by this header:
Harmonic Vibro-Rotational Analysis
If anharmonic analysis is requested as well (i.e., VibRot and Anharmonic are both specified), then the anharmonic vibrational-rotational analysis results follow the harmonic ones, introduced by the following header:
Second-order Perturbative Anharmonic Analysis
Anharmonic Frequency Calculations. Freq=Anharmonic jobs produce additional output following the normal frequency output. (It follows the vibrational-rotational coupling output if this was specified as well.) We will briefly consider the most important items.
The output displays the equilibrium geometry (i.e., the minimum on the potential energy surface), followed by the anharmonic vibrationally averaged structure at 0 K:
Internal coordinates for the Equilibrium structure (Se)
Interatomic distances:
1 2 3 4
1 C 0.000000
2 O 1.206908 0.000000
3 H 1.083243 2.008999 0.000000
4 H 1.083243 2.008999 1.826598 0.000000
Interatomic angles:
O2-C1-H3=122.5294 O2-C1-H4=122.5294 H3-C1-H4=114.9412
O2-H3-H4= 62.9605
Dihedral angles:
H4-C1-H3-O2= 180.
Internal coordinates for the vibrationally average structure at 0K (Sz)
Interatomic distances:
1 2 3 4
1 C 0.000000
2 O 1.210431 0.000000
3 H 1.097064 2.024452 0.000000
4 H 1.097064 2.024452 1.849067 0.000000
Interatomic angles:
O2-C1-H3=122.57 O2-C1-H4=122.57 H3-C1-H4=114.8601
O2-H4-H3= 62.8267
Dihedral angles:
H4-C1-H3-O2= 180.
Note that the bond lengths are slightly longer in the latter structure. The predicted coordinates at STP follow in the output.
The anharmonic zero point energy is given shortly thereafter in the output:
Anharmonic Zero Point Energy ---------------------------- Harmonic : cm-1 = 5008.40626 ; Kcal/mol = 14.320 ; KJ/mol = 59.914 Anharmonic Pot.: cm-1 = -53.31902 ; Kcal/mol = -0.152 ; KJ/mol = -0.638 Watson+Coriolis: cm-1 = -12.83227 ; Kcal/mol = -0.037 ; KJ/mol = -0.154 Total Anharm : cm-1 = 4942.25496 ; Kcal/mol = 14.131 ; KJ/mol = 59.122
The anharmonic frequencies themselves appear just a bit later in this table, in the column labeled E(anharm):
==================================================
Anharmonic Infrared Spectroscopy
==================================================
Units: Transition energies (E) in cm^-1
Integrated intensity (I) in km.mol^-1
Fundamental Bands
-----------------
Mode(n) E(harm) E(anharm) I(harm) I(anharm)
1(1) 2938.531 2788.983 55.17567187 55.41312200
2(1) 1888.862 1864.231 101.42877427 104.63741421
...
Overtones
---------
Mode(n) E(harm) E(anharm) I(anharm)
1(2) 5877.061 5517.149 0.00211652
2(2) 3777.724 3710.383 3.68324904
...
Combination Bands
-----------------
Mode(n) Mode(n) E(harm) E(anharm) I(anharm)
2(1) 1(1) 4827.393 4654.114 1.74785224
3(1) 1(1) 4490.139 4271.343 0.04557003
...
The harmonic frequencies are also listed for convenience.
Vibronic Analysis. The following input file predicts the vibronic spectrum:
%OldChk=excited Excited state calculation. %Chk=fcht # Freq=(ReadFC,FCHT,ReadFCHT) Geom=AllCheck … TimeIndependent ReadFCHT additional input. Output=Matrix=JK Output Duschinsky matrix and shift vector. final blank line
The molecule specification is taken from the checkpoint file from the excited state, as are the force constants for the excited states.
FCHT analysis produces many results. The final Duschinsky (state overlap) matrix appears as follows:
Final Duschinsky matrix
-----------------------
Note: The normal coordinates of the final state (columns) are expressed
in the basis set of the normal coordinates of the initial state (rows)
1 2 3 4 5
1 -0.539484D+00 0.839747D+00 0.139916D-01 -0.147815D-01 0.167387D-02
2 -0.594185D+00 -0.373849D+00 -0.647845D+00 0.757424D-01 -0.627709D-02
3 0.303582D-01 0.276954D-01 0.572527D-02 0.354162D+00 -0.933518D+00
…
Note that this output reports the value of Jij for each pair of states. Generally, what is plotted is J2.
The locations and intensities of the predicted bands are reported as follows:
==================================================
Information on Transitions
==================================================
Energy of the 0-0 transition: 31327.1976 cm^(-1)
NOTE: The energy (transition energy) refers to the relative energy,
with respect to the 0-0 transition energy.
The intensity is the line intensity.
DipStr is the dipole strength.
Energy = 0.0000 cm^-1: |0> -> |0> Frequency and transition (states).
-> Intensity = 7003. (DipStr = 0.9135E-01)
Energy = 457.9310 cm^-1: |0> -> |9^1> Location is ~31875 cm-1.
-> Intensity = 650.2 (DipStr = 0.8360E-02) Intensity in dm3cm-1mol-1;
… Dipole strength in au.
The final predicted spectrum follows in a form suitable for plotting:
==================================================
Final Spectrum
==================================================
Band broadening simulated by mean of Gaussian functions with
Half-Widths at Half-Maximum of 135.00 cm^(-1)
Legend:
-------
1st col.: Energy (in cm^-1)
2nd col.: Intensity at T=0K
Intensity: Molar absorption coefficient (in dm^3.mol^-1.cm^-1)
-----------------------------
30327.1976 0.000000D+00
…
31319.1976 0.699549D+04
31327.1976 0.701428D+04
31335.1976 0.699927D+04
…
Resonance Raman Spectra. The following input file computes the resonance Raman intensities from two previously run frequency calculations.
%Chk=S0_freq Ground state checkpoint file. # Freq=(FC,ReadFC,ReadFCHT) Geom=AllCheck … TimeIndependent ReadFCHT additional input. Spectroscopy=ResonanceRaman Predict resonance Raman spectrum. Spectrum=(Lower=800.,Upper=2800.,Broadening=Stick) Spectrum specifications. Intermediate=Source=Chk Get second state data from checkpoint file (named below). RR=(OmegaMin=55000,OmegaMax=56000,OmegaStep=100) RR analysis parameters: ω range and step size. S2_freq.chk Excited state checkpoint file.
See the section on Freq=ReadFCHT for details about the additional input. For each of the Raman modes, the following output appears for each point in the specified range of incident energies (omega):
==================================================
Information on Transitions
==================================================
Energy of the 0-0 transition: 54854.2397 cm^(-1)
Alp2: alpha^2, BsAl: beta_s(alpha)^2, BaAl: beta_a(alpha)^2
Energy = 0.0000 cm^-1: |0> -> |0> Relative energy and involved states.
-> Omega = 55000.0 cm^-1, Sigma = 1.1332
Alp2 = 0.33009E+02, BsAl = 0.29859E+03, BaAl = 0.00000E+00
Following this output, the same data is presented in a tabular form:
==================================================
Final Spectrum
==================================================
No band broadening applied (stick spectrum)
Legend:
-------
1st col.: Raman shift (in cm^-1)
2nd col.: Intensity at T=0K for incident energy: 55000.00 cm^-1
3rd col.: Intensity at T=0K for incident energy: 55100.00 cm^-1
4th col.: Intensity at T=0K for incident energy: 55200.00 cm^-1
5th col.: Intensity at T=0K for incident energy: 55300.00 cm^-1
Raman scattering intensity in cm^3.mol^-1.sr^-1
-----------------------------------------------------------------------------
…
1188.0000 0.000000D+00 0.000000D+00 0.000000D+00 0.000000D+00
1190.0000 0.134622D-21 0.213038D-21 0.358179D-21 0.644832D-21
1192.0000 0.000000D+00 0.000000D+00 0.000000D+00 0.000000D+00
…
Since no spectral broadening was requested here (Spectrum=Broadening=Stick), the only rows with non-zero intensities correspond to the Raman active frequencies.
Examining Low-Lying Frequencies. The output from the full force constant matrix diagonalization (the default Freq=DiagFull), in which the rotational and translational degrees of freedom are retained, appears as following in the output:
Low frequencies --- -19.9673 -0.0011 -0.0010 0.0010 14.2959 Low frequencies --- 25.6133 385.4672 988.9028 1083.0692
This output is from an Opt Freq calculation on methanol. Ignoring sign, there are 3 low-lying modes, located at around 14, 19, and 25 wavenumbers (in addition to the three that are ~0). However, if we rerun the calculation using tight optimization criteria (Opt=Tight) and a larger integration grid, the lowest modes become:
Low frequencies --- -7.4956 -5.4813 -2.6908 0.0003 0.0007 Low frequencies --- 0.0011 380.1699 988.1436 1081.9083
The low-lying modes are now quite small, and the lowest frequencies have moved slightly as a result.
This analysis is especially important for molecular systems having frequencies at small wavenumbers. For example, if the lowest reported frequency is around 30 and there is a low-lying mode around 25 as above, then the former value is in considerable doubt (as is whether the molecular structure is even a minimum).
Rerunning a Frequency Calculation with Different Thermochemistry Parameters. The following two-step job contains an initial frequency calculation followed by a second thermochemistry analysis using a different temperature, pressure, and selection of isotopes:
%Chk=freq
# B3LYP/6-311+G(2d,p) Freq
Frequencies at STP
molecule specification
-Link1-
%Chk=freq
%NoSave
# B3LYP/6-311+G(2d,p) Freq(ReadIso,ReadFC) Geom=Check
Repeat at 300 K
0,1
300.0 1.0
16
2
3
…
Note also that the freqchk utility may be used to rerun the thermochemical analysis from the frequency data stored in a Gaussian checkpoint file.
ReadAnharm Input
Keywords available in the L717 section
The following keywords for specifying various aspects of Freq=Anharm calculations are included as additional input within the Gaussian input file. They control various aspects of anharmonic frequency analyses. Note that these keywords are completely different from those supported in Gaussian 09 (a few of these changes were introduced in Gaussian 09 revision D.01).
Data Sources and Format
The DataSrc, DataAdd and DataMod input items locate the various data required by the anharmonic frequency analysis. They each take a list of parameters and associated values which specify locations from which to retrieve different data items. In general, parameters specify what data is to be read and their values specify the location of that data. The available options for the latter are listed below. Generally, they may be optionally followed by a format suffix.
Source keywords are used to specify where the data is located:
- Src: Use data from the RWF file for the current job. RWF is a synonym.
- Chk: Retrieve data from the current checkpoint file (as defined with %Chk or %OldChk).
- In: Read data from the input stream.
- InChkn: Retrieve data from the nth file in the file list (see the discussion of additional input sections below). Valid values of n run from 1 to 6.
Format Suffixes are appended directly to the source item, and they specify a non-default format for various read-in data. For example, InQMW says to read derivative data from the input stream in mass-weighted normal coordinates. The following suffixes are available:
- QMW: Derivatives are with respect to normal modes in mass-weighted normal coordinates. Q is a synonym for this format suffix.
- QMWX: Harmonic derivatives are with respect to normal modes in Cartesian coordinates, and anharmonic derivatives are with respect to normal modes in mass-weighted normal coordinates. X is a synonym for this format suffix.
- QRedX: Harmonic derivatives are with respect to normal modes in Cartesian coordinates, and anharmonic derivatives are with respect to normal modes in dimensionless normal coordinates.
By default, QMWX is tried first, followed by QMW.
DataSrc=param: Specify the source(s) of various read-in data. The parameter consists of a keyword indicating the data to which it applies and a source keyword indicating its location (and possibly its format). The available parameters are:
- source: Sets the data source for all data.
- Harm=source: Sets the data source for harmonic data. The default is taken from the source file.
- Anharm=source: Sets the data source for harmonic data. The default is taken from the source file.
- Coriolis=source: Sets the data source for the Coriolis couplings. At present, the only supported items are Src and In, and format suffixes may not be used.
- NMOrder=ordering: Specifies the order normal modes are stored in the input source, selected from the following list. This item may be specified in addition to a source item.
- AscNoIrrep: Ascending order. Do not sort by irreducible representation. This is the default.
- Asc: Ascending order. Sort by irreducible representation if possible.
- Desc: Descending order. Sort by irreducible representation if possible.
- DescNoIrrep: Descending order. Do not sort by irreducible representation.
- Print: Use same order as for printing.
The following DataSrc items are deprecated, and are included only for backward similarity to Gaussian 09 (where they functioned as top-level additional input items).
- InDerAU: Use data from the input stream in atomic units.
- InDerAJ: Use data from the input stream in attoJoules
- InDerRed: Use data from the input stream in reduced form. Reduced is an alternate name for this item.
- InDerGau: Use data from the input stream with the layout of the Gaussian output. InGauDer is an alternate name for this item.
DataAdd=params: Read alternate data to replace or complete the original data. Using this option will replace the already existing information in the original data with the data specified here.
- Freq: Replace harmonic frequencies with values given in the input stream (in cm-1). A data source may also be specified as a parameter: Freq=source, but format suffixes are not allowed.
- PESFull=sources: Read force constraints from specified specified source.
- PESHarm=sources: Read harmonic force constants from specified specified source.
- PESAnh=sources: Read anharmonic force constants from specified specified source.
- EDipFull=sources: Read the electric dipole from the specified specified source.
- EDipHarm=sources: Read the harmonic components of the electric dipole from the specified specified source.
- EDipAnh=sources: Read the anharmonic components of the electric dipole from the specified specified source.
- MDipFull=sources: Read the magnetic dipole from the specified source.
- MDipHarm=sources: Read the harmonic components of the magnetic dipole from the specified source.
- MDipAnh=sources: Read the anharmonic components of the magnetic dipole from the specified source.
- PolFull=sources: Read the polarizability tensor from the specified source.
- PolHarm=sources: Read the harmonic components of the polarizability tensor from the specified source.
- PolAnh=sources: Read the anharmonic components of the polarizability tensor from the specified source.
- MagFFull=sources: Read the magnetic-field properties from the specified source.
- MagFHarm=sources: Read the harmonic components of the magnetic-field properties from the specified source.
- MagFAnh=sources: Read the anharmonic components of the magnetic-field properties from the specified source.
- FreqDepPFull=sources: Read the frequency-dependent properties from the specified source.
- FreqDepPHarm=sources: Read the harmonic components of the frequency-dependent properties from the specified source.
- FreqDepPAnh=sources: Read the anharmonic components of the frequency-dependent properties from the specified source.
DataMod=params: Modify the data in various manners.
- ScHarm=value: Scales harmonic frequencies with a constant scaling factor (default is 1.0).
- NoCor: Discards Coriolis couplings in calculations. By default, all couplings will be retained.
- DerOrder=N: Selects the derivatives order to keep. E.g. DerOrder=123 discards all quartic force constants.
- DerIndex=N: Sets the maximum number of independent indexes for a derivative. E.g. DerIndex=2 keeps kiij but discards kijk.
- SkipPT2=what: Selectively removes derivatives based on the parameter, whose possible values are listed below:
- No: Do not remove the data. This is the default option.
- Modes: Removes the derivatives with respect to any of the normal modes given in the input stream.
- Constants: Removes the derivatives based on the indexes given in the input stream. The input explicitly specifies the force constants (energy derivatives) to be removed. Each line specifies the involved normal modes, with the derivative order implied by the number of indexes. For example, to remove the third derivatives with respect to normal coordinates Q1 Q2 Q5, the input line would be:
1 2 5
- OptModes: Modify derivatives based on additional instructions in the input stream (see input ordering section below).
Tolerances=data: Modify the tolerance threshold to include/discard derivative data.
- Gradient=value: Threshold for the energy first derivatives (default is 3.7074×10−3).
- Hessian=value: Threshold for the energy second derivatives (default is 3.7074×10−5).
- Cubic=value: Threshold for the energy third derivatives (default is 3.7074×10−5).
- Quartic=value: Threshold for the energy fourth derivatives (default is 3.7074×10−5).
- Coriolis=value: Threshold for the Coriolis couplings (default is 1.0×10−3).
- Inertia=value: Threshold for the principal moments of inertia (default is 1.0×10−4Å2).
- Symm=value: Tolerance for anharmonic data with respect to symmetry rules (default is 2%).
Output Control
This section specifies the contents and destination of the calculation output.
Print=items: Include items in the output file. Available items are the following:
- InDataX: Include data compatible with DataSrc=InQMWX. The form Print=InDataX=Ext writes the data to the external file input_data.dat.
- InDataNM: Include data compatible with DataSrc=InQMW. The form Print=InDataNM=Ext writes the data to the external file input_data.dat
- YMatrix: Include the Y matrix (a variant of the χ matrix).
- Verbosity=n: Specify the verbosity level. The default is 0.
- ITop=rep: Selects the representation used for rotational spectroscopy. By default, it is defined automatically by Gaussian from the principal moments of inertia. Available representations are:
- Ir: Ir Representation: Iz < Ix < Iy
- IIr: IIr Representation: Iy < Iz < Ix
- IIIr: IIIr Representation: Ix < Iy < Iz
- Il: Il Representation: Iz < Iy < Ix
- IIl: IIl Representation: Ix < Iz < Iy
- IIIl: IIIl Representation: Iy < Ix < Iz
- ZAxisSymm=axis: Sets the Eckart axis to be used as Z for the definition of the reduced Hamiltonians for the vibrorotational analysis. Available choices are:
- X: Z collinear with X.
- Y: Z collinear with Y.
- Z: Z collinear with Z.
- NMOrder=ordering: Specifies the order in which normal modes are listed:
- Asc: Ascending order. Sort by irreducible representation if possible.
- Desc: Descending order. Sort by irreducible representation if possible. This is the default.
- AscNoIrrep: Ascending order. Do not sort by irreducible representation.
- DescNoIrrep: Descending order. Do not sort by irreducible representation.
- PT2VarEVec: Include the eigenvector matrix from the diagonalization of the variational matrix.
- PT2VarStates: Include the projection of the variational states on the deperturbed ones.
- PT2VarProj: Include the projection of the DVPT2 states on the new variational states.
- InDataAU: Write data compatible with DataSrc=InDerAU (deprecated).
- Polymode: Write data to use in the Polymode program.
Reduced-Dimensionality Schemes
RedDim=items: Specifies which normal modes are active in the analysis. Items are:
- Active=n: Activate the n modes specified in the input stream. By default, all modes are active.
- Inactive=n: Read list of n inactive modes from the input stream.
- Frozen=n: Read n modes to be frozen from the input stream.
- MinFreqAc=freq: Sets the normal modes with a frequency above the specified value to be active (default is 0). Only valid if MaxFreqAc>MinFreqAc.
- MaxFreqAc=freq: Sets the normal modes with a frequency below the specified value to be active (default is infinity). Only valid if MaxFreqAc>MinFreqAc.
- MinFreqIn=freq: Sets the normal modes with a frequency above the specified value to be inactive (default is 0). Only valid if MaxFreqIn>MinFreqIn.
- MaxFreqIn=freq: Sets the normal modes with a frequency below the specified value to be active (default is infinity). Only valid if MaxFreqIn>MinFreqIn.
- MinFreqFr=freq: Sets the normal modes with a frequency above the specified value to be frozen (default is 0). Only valid if MaxFreqFr>MinFreqFr.
- MaxFreqFr=freq: Sets the normal modes with a frequency below the specified value to be frozen (default is infinity).Only valid if MaxFreqFr>MinFreqFr.
Second-Order Vibrational Perturbation Theory (VPT2)
PT2Model=data: Sets the VPT2 model to use. The default is GVPT2.
- HDCPT2: Use the Hybrid Degeneracy-Corrected 2nd-order Perturbation Theory.
- VPT2: Use the original 2nd-order Vibrational Perturbation Theory. Vibrational spectroscopy intensities are available for this model.
- DVPT2: Use the Deperturbed 2nd-order Vibrational Perturbation Theory. Vibrational spectroscopy intensities are available for this model. The form DVPT2=all selects all possibly resonant terms as Fermi resonances, and it is equivalent to Resonances=(DFreqFrm=∞,DPT2Var=0.)
- GVPT2: Use the Generalized 2nd-order Vibrational Perturbation Theory. This is the default. It is similar to DVPT2, but the removed terms are treated variationally in a second step. Vibrational spectroscopy intensities are available for this model. The form GVPT2=all selects all possibly resonant terms as Fermi resonances, and it is equivalent to Resonances=(DFreq12=∞,K12Min=0.)
- DCPT2: Use the Degeneracy-Corrected 2nd-order Perturbation Theory.
HDCPT2=params: Set the parameters for the model with the Alpha and Beta options (i.e., HDCPT2=Alpha=value), which specify values for the corresponding variables in the expression for Λ: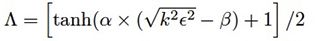
Resonances=params: Set resonance thresholds and parameters for DVPT2 (Fermi-related items only) and GVPT2 calculations.
- DFreq12=value: Sets the maximum frequency for 1–2 Fermi resonances (ωi-(ωj+ωk)). The default is 200 cm-1.
- DFreq22=value: Sets the maximum frequency for 2–2 Darling-Dennison resonances (2ωi-(ωj+ωk) and 2ωi-2ωj). The default is 100 cm-1.
- DFreq11=value: Sets the maximum frequency for 1–1 Darling-Dennison resonances (ωiωj). The default is 100 cm-1.
- DFreq13=value: Sets the maximum frequency for 1–3 Darling-Dennison resonances (ωi-(ωj+ωk+ωl)). The default is 100 cm-1.
- K12Min=value: Sets the maximum allowed difference between the VPT2 and model variational results (Martin test). The default is 1 cm-1.
- K22Min=value: Sets the minimum value for off-diagonal 2–2 Darling-Dennison term. The default is 10 cm-1.
- K11Min=value: Sets the minimum value for off-diagonal 1–1 Darling-Dennison term. The default is 1 cm-1.
- K11MinI=value: Sets the minimum value for the secondary 1–1 resonance test, intended to detect critical cases specific to intensity calculations. The default is 1 cm.
- K13Min=value: Sets the minimum value for off-diagonal 1–3 Darling-Dennison term. The default is 10 cm-1.
- K13MinI=value: Sets the minimum value for the secondary 1–3 resonance test, intended to detect critical cases specific to intensity calculations. The default is 0.25 cm.
- HDCPT2=value: Sets the minimum value for the HDCPT2/VPT2 difference test. The default is 0.1.
- NoFermi: Deactivates the search for 1–2 Fermi resonances. No12Res is a synonym for this item.
- NoDarDen: Deactivates the search for Darling-Dennison (2–2, 1–1 and 1–3) resonances.
- No22Res: Deactivates the search for 2–2 Darling-Dennison resonances.
- No11Res: Deactivates the search for 1–1 Darling-Dennison resonances.
- No13Res: Deactivates the search for 1–3 Darling-Dennison resonances. 1–3 resonances are only available for 3-quanta transitions.
- List=action: Tells Gaussian to read resonance cases from the input stream. action is optional; it defaults to Replace. Otherwise, it controls the use of the input resonances. The available action keywords are:
- Replace: Discards automatic analysis and only use resonances in the input. This is the default.
- Add: Augments automatic results with input data. A simpler form of this option is Resonances=Add.
- Delete: Remove resonances in the input list from the results of the automatic analysis. A simpler form of this option is Resonances=Delete.
- Modify: Add or remove resonances starting from the list obtained from the automatic analysis. An action keyword—ADD or DEL—must precede the resonance data on each input line.
See the Specifying Resonances subsection below for more information.
Spectroscopy
Spectro=MaxQuanta=quanta: Compute transition integrals to states with up to the specified quanta. The default is 2.
ROA=params: Options related to Raman optical activity. If the keyword is specified, then only those scatterings explicitly requested will be computed. If the ROA is not specified, then intensities are computed for all supported scatterings.
- ICP0: Compute ROA intensity for ICP forward scattering.
- ICP90x: Compute ROA intensity for incident circular polarization (ICP) right-angle scattering (polarized).
- ICP90z: Compute ROA intensity for ICP right-angle scattering (depolarized).
- ICP90*: Compute ROA intensity for ICP right-angle scattering (magic angle).
- ICP180: Compute ROA intensity for ICP backward scattering.
- SCP0: Compute ROA intensity for scattered circular polarization(SCP) forward scattering.
- SCP90x: Compute ROA intensity for SCP right-angle scattering (polarized).
- SCP90z: Compute ROA intensity for SCP right-angle scattering (depolarized).
- SCP90*: Compute ROA intensity for SCP right-angle scattering (magic angle).
- SCP180: Compute ROA intensity for SCP backward scattering.
- DCP180: Compute ROA intensity for double circular polarization (DCP) backward scattering.
- All: Compute the ROA intensity for all supported scatterings.
Freq=ReadAnharm Additional Input Ordering
The potential input sections for the various Freq=ReadAnharm additional input items should follow the keyword list section in the following order. Blank lines separate input sections, but each section and its terminating blank line should be included only when the corresponding keyword is specified.
Freq=ReadAnharm input keywords
blank line
checkpoint file list for DataSrc=InChkn or DataAdd=…=InChkn
blank line
data for DataSrc=In or DataAdd=…=In (harmonic followed immediately by anharmonic)
blank line
data for DataAdd=Freq
blank line
n modes for RedDim=Active
blank line
n modes for RedDim=Inactive
blank line
n modes for RedDim=Frozen
blank line
keyword for DataMod=SkipPT2=OptModes (see below)
modes for DataMod=SkipPT2=Modes or Constants or DataMod=SkipPT2=OptModes
blank line
data for Resonances=List
blank line
DataMod=SkipPT2=OptModes Keywords: Removal of Contributions from Selected Normal Modes
One or more options are specified on a single line with no blank line following. The options available are:
- MinInd=n: Controls the minimum number of times a selected normal mode must appear to discard the derivative. The default is 1. For example, a value of 2 means that kijk is kept, but kiij and kiii are removed.
- EnOrd=mask: Controls the energy derivative orders to consider. The default is 1234 which says to include all energy derivatives. The value 14 says to only treat the first and fourth energy derivatives and to ignore the second and third energy derivatives.
Here is an example calculation using DataMod=SkipPT2=OptModes:
# Freq=(Anharm,ReadAnharm) … Formaldehyde 0 1 C -0.6067825443565 -0.0000000216230 0.0000000000000 O 0.6033290944914 0.0000000215000 0.0000000000000 H -1.1752074085613 0.9201232113261 0.0000000000000 H -1.1752073429832 -0.9201232950844 0.0000000000000 PT2Model=GVPT2 Resonances=(NoDarDen,NoFermi) DataMod=SkipPT2=OptModes MinInd=2 EnOrd=34 Control keywords: keep only kijk for third and fourth derivatives 5 6 Modes for which to remove derivatives terminating blank line
Specifying Resonances
For Resonances=Add, Resonances=List=Replace and Resonances=Delete, each line contains the type of resonance and the indexes of the normal modes involved in the resonances. Supported types are:
- 1-2 or 12: 1-2 Fermi resonance. 3 indexes needed, given in the order: ω1 ≈ ω2 + ω3
- 1-1 or 11: 1-1 Darling-Dennison resonance. 2 indexes needed, given in the order: ω1 ≈ ω2
- 1-3 or 13: 1-3 Darling-Dennison resonance. 4 indexes needed, given in the order: ω1 ≈ ω2 + ω3 + ω4
- 2-2 or 22: 2-2 Darling-Dennison resonance. 4 indexes needed, given in the order: ω1 + ω2 ≈ ω3 + ω4
For Resonances=List=Modify, an action must be specified at the beginning of the line, before the resonance type and the normal modes. The available actions are ADD (add resonance) and DEL (remove resonance if previously identified).
Examples
Example 1: Frequency data calculated in the current job:
%Chk=example1 # B3LYP/6-311+G(d,p) Freq=(Anharmonic,ReadAnharm) Anharmonic frequencies example 1 molecule specification DataMod=SkipPT2=Modes Freq=ReadAnharm additional input RedDim=Inactive=1 # modes to make inactive PT2Model=GVPT2 Resonances=Add Print=InDataX=Ext Write data to an external file blank line 6 Modes to make inactive: RedDim=Inactive blank line 4 5 Modes for which to discard derivatives: DataMod=SkipPT2=Modes blank line 1-2 2 3 3 List of additional resonances: Resonances=Add blank line
Example 2: Frequency data read from input stream. It uses the checkpoint file from Example 1 to retrieve the molecular geometry and Hessian:
%OldChk=example1 %Chk=example2 # B3LYP/6-311+G(d,p) Freq=(ReadFC,Anharmonic,ReadAnharm) Geom=Check Anharmonic frequencies example 2 0 1 PT2Model=GVPT2 Freq=ReadAnharm additional input DataSrc=(InQMWX,NMOrder=Desc) Read harmonic/anharmonic data from input DataAdd=Freq Replace harmonic frequencies with input values RedDim=Inactive=1 blank line @input_data.dat Data file from previous job with Print=InDataX=Ext blank line 1198.351 List of harmonic frequencies: DataAdd=Freq 1259.285 1530.636 1814.590 2884.164 2941.556 blank line 6 blank line
Example 3: The following example specifies alternate values for several parameters:
# B3LYP/6-31G(d) Freq=(Anharm,ReadAnharm) Anharmonic frequencies example 3 molecule specification Tolerances=Coriolis=0.25 Freq=ReadAnharm additional input Resonances=(DFreq12=220.0,K12Min=1.1) DataMod=SCHarm=0.98 blank line
Example 4: Anharmonic VCD and ROA spectra calculation:
%Chk=project4 # Freq=(ROA,VCD,Anharm,ReadAnharm) CPHF=RdFreq … Anharmonic VCD and ROA spectrum 0 1 molecule specification 589.3nm incident light frequency PT2Model=GVPT2 ReadAnharm input section Spectro=MaxQuanta=3 blank line
ReadFCHT Input
Keywords Available in the L718 Section
The following keywords for specifying various aspects of Freq=FC, HT or FCHT calculations are included as additional input within the Gaussian input file. They control various aspects of these analyses. Note that these keywords are different from those supported in Gaussian 09.
Specifying Calculation Options and Parameters
Transition=type: Specify the type of electronic transition.
- Absorption: Absorption. This is the default.
- Emission: Emission.
Spectroscopy=type(s): Spectroscopy to simulate. The default is Spectroscopy=OnePhoton. The following items are available (names may be abbreviated to just the capital letters below: e.g., RR for ResonanceRaman):
- OnePhoton: One-photon process. This is the default.
- CircularDichroism: Circular Dichroism: electronic circular dichroism (ECD) for absorption and circularly polarized luminescence (CPL) for emission.
- OnePhotonAbsorption: One-photon absorption. Implies Transition=Absorption.
- OnePhotonEmission: One-photon emission. Implies Transition=Emission.
- ElectronicCircularDichroism: Electronic circular dichroism. Implies Transition=Absorption.
- CircularlyPolarizedLuminescence: Circularly polarized luminescence. Implies Transition=Emission.
- ResonanceRaman: Vibrational Resonance Raman. Options are specified via a separate item (see below).
ResonanceRaman=options: The following RR-specific options are available:
- CombOnly: Compute only combination bands.
- NoComb: Skip computation of combination bands.
- aMean=coeff: Set the coefficient of the mean polarizability. The default is 45.
- Damping=value: Damping constant or lifetime of intermediate states (in cm−1). The default is 500 cm-1.
- dAnti=coeff: Set the coefficient of the antisymmetric anisotropy. The default is 5.
- gSymm=coeff: Set the coefficient of the symmetric anisotropy. The default is 7.
- Omega=value: Incident energy (in cm−1). By default, it is calculated as the difference in energy between the vibrational fundamental states of the initial and intermediate states.
- OmegaList: Reads a list of incident energies (in cm−1) in the input stream to build an energy profile.
- OmegaMax=value: Maximum energy (in cm−1) for the incident energy profile.
- OmegaMin=value: Minimum energy (in cm−1) for the incident energy profile.
- OmegaNum=n: Number of energies in the incident energy profile.
- OmegaStep=value: Energy interval (in cm−1) between two energies for the incident energy profile.
- Scattering=params: Scattering geometry for the Resonance Raman simulation. Available items are (note that the asterisks below are part of the parameter names):
- ICP0: Compute RR intensity for Incident Circular Polarization (ICP) forward scattering.
- ICP90x: Compute RR intensity for ICP right-angle scattering (polarized).
- ICP90z: Compute RR intensity for ICP right-angle scattering (depolarized).
- ICP90*: Compute RR intensity for ICP right-angle scattering (magic angle).
- ICP180: Compute RR intensity for ICP backward scattering.
- SCP0: Compute RR intensity for Scattered Circular Polarization (SCP) forward scattering.
- SCP90x: Compute RR intensity for SCP right-angle scattering (polarized).
- SCP90z: Compute RR intensity for SCP right-angle scattering (depolarized).
- SCP90*: Compute RR intensity for SCP right-angle scattering (magic angle).
- SCP180: Compute RR intensity for SCP backward scattering.
- DCP180: Compute RR intensity for Double Circular Polarization (DCP) forward scattering.
- All: Compute the RR intensity for all supported scatterings.
Temperature: Specify temperature and related parameters:
- Value=temp: Temperature of simulation in K. The default is the value specified to Gaussian with the Temp keyword or via additional input; the Gaussian default is 298.15 K.
- MinPop=ratio: Minimum ratio between the Boltzmann populations of any vibrational initial state and the fundamental state for the former to be considered in the calculations. In other words, this item specifies the fraction of a vibrational state that must be populated in order for it to be treated as the starting point of a transition. The default value is 0.1 (10%).
TransProp=definition: Definition of the transition dipole moment(s). The first three items effectively select among Franck-Condon, Herzberg-Teller and FCHT analyses. However, the corresponding options to the Freq keyword are preferable. The following items are available:
- FC: The dipole moment is assumed constant during the electronic transition. This selection describes dipole-allowed transitions well. It is the default.
- FCHT: Computes zeroth- and first-order terms of the Taylor expansion of the transition dipole moment about the equilibrium geometry. It is needed to correctly treat weakly-allowed electronic transitions or CD spectra.
- HT: Implements linear variation of the dipole moment with respect to the normal mode. This item corresponds to the first-order term of the Taylor expansion of the transition dipole moment about the equilibrium geometry.
- DipA=source: Explicit definition of the transition dipole moment dA. The following options for the data source are available:
- Auto: Gaussian will choose the definition depending on the simulation parameters. This is the default.
- Read: Read data from main input source (see “Data Sources” below).
- Input: Read data from input stream.
- DipB=source: Definition of the transition dipole moment dB. This item accepts the same data source options as DipA.
- EDip=source: Definition of the transition electric dipole moment. This item accepts the same data source options as DipA.
- MDip=source: Definition of the transition magnetic dipole moment. This item accepts the same data source options as DipA.
- NoUse: Discard the transition dipole read in the data source and replace it with a unitary one. This is the default behavior for electronic transition with a change in multiplicity or charge. Keyword is not supported for HT and FCHT calculations.
Method=method: Selects the representation model for the electronic transition. The non-default options specify methods for approximating the excited state frequencies based on the ground state. These are not generally preferable to modeling the excited state explicitly. The following methods are available:
- AdiabaticHessian: Both PESs—ground state and excited state—are calculated at the harmonic level about their respective minimum. This is the default.
- AdiabaticShift: Both PESs are calculated at the harmonic level about their respective minimum, but the PES of the final state is assumed to be the same as the initial state. Only the equilibrium geometry of the final state is calculated.
- VerticalHessian: The PES of the final state is evaluated about the equilibrium geometry of the initial state.
- VerticalGradient: The PES of the final state is evaluated about the equilibrium geometry of the initial state, but the PES of the final state is assumed to be the same as the initial state. Only the energy gradient of the final state is calculated about the equilibrium geometry of the initial state. (This method is also known as the linear coupling model.)For emission spectra, the form VerticalGradient=Abs causes Gaussian to compute the 0-0 transition energy in the same way as absorption spectra in order to get the correct 0-0 transition energy. It is needed when the emission spectrum is incorrectly computed as an absorption spectrum (equilibrium geometry of the ground state, frequencies of the ground state and forces of the excited state).
Prescreening=params: Sets the prescreening criteria for choosing the most intense transitions. Only available for the time-independent framework. Available parameters:
- MaxC1=n: Maximum quantum number reached in C1 (C1max). The default is 20.
- MaxC2=n: Maximum quantum number reached by both modes involved in the combination bands in C2 (C2max). The default is 13.
- MaxInt=millions: Maximum number of integrals to compute for each class above C2 (NImax), in units of one million. The default value is 100 (100,000,000).
TimeIndependent: Use the time-independent framework. This is the default for one-photon spectroscopy. TI is a synonym for this item.
TimeDependent=params: Compute the band shape using the path-integral approach instead of the sum-over-states approach. This is the default for Resonance Raman spectroscopy. TD is a synonym for this item. Available parameters are:
- 2NStep=m: Use 2m steps for the integration. m defaults to 18 for OPA, OPE, ECD and CPL and 12 for RR.
- 2NStepWin=k: Set the number of steps in which the correlation function Χ(t) is actually computed to as 2k. The function is 0 outside this range. Note that k must be ≤ m from 2NStep above. By default, k is set equal to m.
- GauHWHM=n: Inhomogenous broadening, applied as a dephasing (in cm−1). The default is 135 cm−1.
- LorHWHM=n: Homogenous broadening, applied as a dephasing (in cm−1). The default is 0 cm−1.
- Time=seconds: Time interval Δt in seconds. The default value is 2m×10-17, where m is from 2NStep above.
Termination=DeltaSP=value: Sets the termination criteria. Set the minimum difference between two consecutive classes of the final state to continue the calculation. The default is 0.0 (always continue).
Data Sources
The items in this section specify the locations and methods for obtaining various data used by the FCHT analysis.
Initial=items: Data source(s) and/or parameters for the initial state.
Final=items: Data source(s) and/or parameters for the final state.
Intermediate=items: Data sources(s) and/or parameters related to the intermediate state. Only valid for Resonance Raman.
The following parameters are available for the three preceding items:
- Source=source: Data source for the state:
- Calc: Current calculation. This is the default for Absorption spectra.
- Chk: Checkpoint file (the filename is given in the input stream). This is the default for Emission spectra.
- LogFile: Gaussian output filename (the filename is given in the input stream).
- Freq=params: Source and handling of vibrational frequency data:
- Read: Read frequencies from the main data source. This is the default.
- Input: Read frequencies from the input stream.
- Scale: Scale frequencies using a mode-specific extrapolated scaling factor based on the Duschinsky transformation. The reference state used is the other electronic state. For example, Final=Freq=Scale uses the input initial state frequencies to scale those of the final state. The required frequencies are taken from the input stream in their usual position (see below).
- MaxBands=state: Set the highest class state to consider. The default is 3 for Initial and 7 otherwise.
- MaxStates=n: Maximum number of initial vibrational states actually considered in the calculations. Only valid with Initial. Note that this value is not the number of configurations printed by Gaussian. The default is 50.
- ExcState=state: Excited electronic state actually treated in the Gaussian output file. Only used if the data source for the excited state is a Gaussian output file.
DataAdd=DeltaE=value: Difference in energy between the electronic states (in Hartrees). By default, it is calculated from the data sources used for the initial and final states.
DataMod=Duschinsky=params: Duschinsky matrix to use in the calculation, By default, the true Duschinsky matrix is used. Note that the definition of the Duschinsky matrix depends on the model used to describe the transition. Other options are:
- Identity: Use the identity matrix as the Duschinsky matrix.
- Diagonal: Swap the columns of the correct Duschinsky matrix to be as diagonal as possible and replace it by the identity matrix. If this cannot be done because the matrix is not diagonal enough, an error occurs.
Superpose=param: Specify the superposition procedure.
- Reorient: Reorient molecules to maximize overlap between the two structures. This is the default.
- NoReorient: Do not try to superpose the structures.
- Rotation=n: Rotation algorithm used for the superposition:
- 0: Alternate usage. First quaternions, then rotation angles. This is the default.
- 1: Use the program default (be aware that this may change between Gaussian versions).
- 2: Use quaternions only.
- 3: Use rotation angles only.
- RotNIter=xxxyyy: Maximum number of iterations for each superposition algorithm, where xxx is the number of iterations for the algorithm based on quaternions, and yyy is the number of iterations for the angle-based algorithm. The default parameter is 030100 or 30 for quaternions and 100 for rotation angles.
Output Selection
Print=params: This item controls the information included in the output.
- Spectra=params: Spectra to be included (the non-default items are not valid in the time-dependent framework nor for Resonance Raman):
- Final: Print only the final spectrum. This is the default.
- All: Print the maximum number of class-specific spectra.
- ClassI: Print one spectrum for each class of the initial state.
- ClassF: Print one spectrum for each class of the final state.
- Matrix=list: Matrices to be displayed: J, K, A, B, C, D, E. The string is composed of the matrices of interest, e.g., JK. A, B, C, D and E are the Sharp and Rosenstock matrices, J is the Duschinsky matrix, and K is the shift vector.
- HuangRhys: Print Huang-Rhys factors [Huang50].
- AssignThresh=n: Include data (assignment, energy, intensity) of the transitions, which contribute at least to 100n% to the total intensity of the spectrum obtained for each initial vibrational state. The default is 0.01 (1%).
- TDAutoCorr=n: Print n points of the time-dependent autocorrelation function. The default is 0 (output disabled).
- Tensors: Print the transition tensors instead of the invariants. Only available for Resonance Raman.
- Conver: Print convergence data. Only available for Resonance Raman.
- Color=params: Specify RGB standard for color output:
- sRGB: Use the sRGB standard (white reference: D65, gamma correction based on the IEC 61966-2-1 standard). This is the default.
- None: Do not print the color in an RGB format.
- CIE: Use the CIE RGB standard (white reference: D65, no gamma correction).
- HDTV: Use the HDTV RGB standard (white reference: D65, gamma correction based on the ITU-R BT.709-3 standard).
Spectrum=params: Control spectrum layout.
- Lower=value: Energy of the lower bound of the spectrum (in cm−1). For absorption, the default is -1000 cm−1. For emission, the default is -8000 cm−1. The bound is defined with respect to the 0-0 transition.
- Upper=value: Energy of the upper bound of the spectrum (in cm−1). For absorption, the default is +8000 cm−1. For emission, the default is +1000 cm−1. The bound is defined with respect to the 0-0 transition.
- AbsBounds: Deactivate the default behavior of Gaussian to define the lower and upper bounds of the spectrum with respect to the 0-0 transition.
- Grain=value: Energy difference between two adjacent points for the discretization of the spectrum (in cm−1). The default is 8cm-1.
- Broadening=params: Discribution function used to compute the band-shape:
- Gaussian: Use normal distribution functions to simulate the inhomogeneous broadening. This is the default.
- Lorentzian: Use Cauchy distribution functions to simulate the homogeneous broadening.
- Stick: Do not simulate the band broadening. Print the bands as sticks.
- HWHM=value: Half-width at half-maximum of the distribution function used for the convolution (in cm−1). The default is 135 cm-1.
Reduced-Dimensionality Schemes
RedDim=params: Activates and sets a reduced-dimensionality scheme.
- Block: Use the correct Duschinsky matrix to find the projection of a list of modes given in the input stream on the other state to reduce consistently the dimension of the problem. By default, the state of reference is the lower one.
- ClearLowFreq=n: Remove all normal modes with a frequency below n cm−1 in absolute value. If this parameter is specified but n is omitted, it defaults to 50.
- ClearImFreq: Remove at most one normal mode per state with an imaginary frequency. If there is one mode with an imaginary frequency in each state, Gaussian checks that they are uncoupled to other modes and project themselves on each other in the electronic transition.
- BlockThresh=value: Threshold for the block(s) construction (between 0 and 1). A high value ensures that the selected modes are uncoupled from the remaining ones. The default is 0.9.
- BlockTol=n: Specifies the maximum ratio allowed between the final number of selected modes and the initial set: if more than n×#modes chosen by the user are selected, Gaussian stops the calculations. The default is 1.6.
Freq=ReadFCHT Additional Input Ordering
The potential input sections for the various Freq=ReadFCHT additional input items should follow the keyword list section in the following order. Blank lines separate input sections, but each section and its terminating blank line should be included only when the corresponding item is specified.
Freq=ReadFCHT input keywords
blank line
filename for the Chk or LogFile parameters to Input=Source
filename for the Chk or LogFile params. to Final=Source (OPA, OPE, ECD, CPL) or Intermediate=Source (RR)
blank line
initial state frequency list: Initial=Freq=Input and/or Final=Freq=Scale
blank line
final/intermediate state frequency list: the Freq=Input option to Final (OPA, OPE, ECD, CPL) or Intermediate (RR) and/or Initial=Freq=Scale
blank line
transition dipole moment data for TransProp=DipA or TransProp=EDip
blank line
transition dipole moment data for TransProp=DipB or TransProp=MDip
blank line
list of modes for RedDim=Block
blank line
incident energies for ResonanceRaman=OmegaList
blank line
Examples
The following input file illustrates the use of additional input for FC analyses.
Example 1. The following calculation performs a Franck-Condon frequency analysis for phenoxyl:
%Chk=phenoxyls0.chk # Freq=(FC,ReadFC,ReadFCHT) Geom=Check … Phenoxyl Frank-Condon analysis 0 2 Final=Source=Chk ReadFCHT input: specify source for final state. Print=(Spectra=All,Matrix=JK) Output all spectra, the Duschinsky matrix and the shift vector. phenoxyls1.chk Checkpoint file for the final state. terminal blank line
Example 2. The following job predicts the ECD spectrum (selected by the item in the additional input section). Note that the second checkpoint file for the final section is specified in the subsequent input section. It is read even though there is no explicit item in the additional input section since Final=Source=Chk is the default for emission spectra.
%Chk=initial # Freq=(FCHT,ReadFC,ReadFCHT) Geom=AllCheck … Transition=Absorption ReadFCHT input. Spectroscopy=CD Select spectrum to predict: ECD. final.chk Checkpoint file for the final state. terminal blank line
Example 3. The following job performs the analysis at 500 K, using the time-dependent framework.
%Chk=temp500init # Freq=(FC,ReadFC,ReadFCHT,SaveNM) Geom=AllCheck … Temperature=Value=500.0 TimeDependent temp500final.chk terminal blank line
Example 4. The following job computes the resonance Raman spectrum:
%Chk=S0_freq # Freq=(FC,ReadFC,ReadFCHT) Geom=Check … RR spectrum 0 1 Spectroscopy=RR ReadFCHT input: select spectrum to predict. TransProp=EDip=Input RR=OmegaList TD=(2NSTEP=12,2NSTEPWIN=12,Time=1.0d-12,GauHWHM=100) Print=(Tensors,Matrix=JK) S2_freq.chk Checkpoint file for final state. 1.000D0 1.000D0 0.00D0 Transition dipole for TransProp=EDip. 55000 55500 57000 List of incident energies for RR=OmegaList. terminal blank line
Example 5. The final job step below computes the vibrational envelope of a photoionization spectrum:
%chk=neutral Calculation on the neutral form (initial state). # B3LYP/6-31+G(d,p) Freq=SaveNM neutral form 0 1 molecule specification --Link1-- %chk=cation Calculation on the cation (final state). # B3LYP/6-31+G(d,p) Freq=SaveNM cation 1 2 molecule specification --Link1-- %oldchk=neutral Data for the neutral form. %chk=fc # B3LYP/6-31+G(d,p) Freq=(FC,ReadFCHT) Geom=Check photoionization 0,1 Initial=Source=Calc Final=Source=Chk Retrieve final state from a checkpoint file. Spectrum=(Lower=-500.,Upper=+5000.,Grain=1.,HWHM=50.) Parameters for computed spectrum. Prescreening=(MaxC1=30.,MaxC2=20.) Parameters to select transitions. Print=Matrix=JK Output Duschinsky matrix and shift vector. cation.chk Checkpoint filename for final state. terminal blank line
Last updated on: 16 December 2020. [G16 Rev. C.01]