
When considering molecular orbitals, it is often useful to examine the contributions of the individual atomic orbitals. Gaussian can provide this information as part of the population analysis.
Specifically, orbital-by-orbital population analysis is requested with the Pop=Orbitals option. This performs a population analysis of the highest N occupied and lowest N virtual orbitals, including the atomic contributions to each MO. If not specified, N defaults to 10. Analysis of all orbitals can be specified by replacing N with a value within Orbitals=N. For open shell calculations, both alpha and beta orbitals are included.
Here we use the uranyl ion—UO22+—as an example for this feature. This system is a singlet dication:
We ran a single point energy calculation using this route section:
# APFD/6-311+G(2d,p) Opt Freq Pop=Orbitals
Here is the Pop=Orbitals output:
Atomic contributions to Alpha molecular orbitals: Alpha occ 14 OE=-1.502 is U1-p=0.7281 U1-f=0.2593 Alpha occ 15 OE=-1.502 is U1-p=0.7281 U1-f=0.2593 Alpha occ 16 OE=-1.480 is O3-s=0.4088 O2-s=0.4088 Alpha occ 17 OE=-1.196 is U1-p=0.3770 O2-s=0.2689 O3-s=0.2689 Alpha occ 18 OE=-0.918 is O2-p=0.3760 O3-p=0.3760 U1-d=0.2100 Alpha occ 19 OE=-0.918 is O3-p=0.3760 O2-p=0.3760 U1-d=0.2100 Alpha occ 20 OE=-0.907 is U1-f=0.3569 O3-p=0.3062 O2-p=0.3062 Alpha occ 21 OE=-0.907 is U1-f=0.3569 O3-p=0.3062 O2-p=0.3062 Alpha occ 22 OE=-0.888 is O2-p=0.3549 O3-p=0.3549 U1-d=0.1439 Alpha occ 23 OE=-0.873 is U1-f=0.5581 O3-p=0.1638 O2-p=0.1638 U1-p=0.1039 Alpha vir 24 OE=-0.682 is U1-f=1.0000 Alpha vir 25 OE=-0.682 is U1-f=1.0000 Alpha vir 26 OE=-0.668 is U1-f=1.0000 Alpha vir 27 OE=-0.668 is U1-f=1.0000 Alpha vir 28 OE=-0.582 is U1-f=0.6313 O3-p=0.1472 O2-p=0.1472 Alpha vir 29 OE=-0.582 is U1-f=0.6313 O2-p=0.1472 O3-p=0.1472 Alpha vir 30 OE=-0.554 is U1-d=0.8198 U1-g=0.1802 Alpha vir 31 OE=-0.554 is U1-d=0.8200 U1-g=0.1800 Alpha vir 32 OE=-0.546 is U1-s=1.4099 U1-d=-0.4559 Alpha vir 33 OE=-0.396 is U1-f=0.4041 O3-p=0.2508 O2-p=0.2508
Note that AO contributions that are less than 10% are not included by default. You can change this threshold with the Pop=ThreshOrbitals option. For example, Pop=ThreshOrbitals=5 would include all contributions of 5% or more in the output.
We illustrate and discuss three of the uranyl molecular orbitals below:
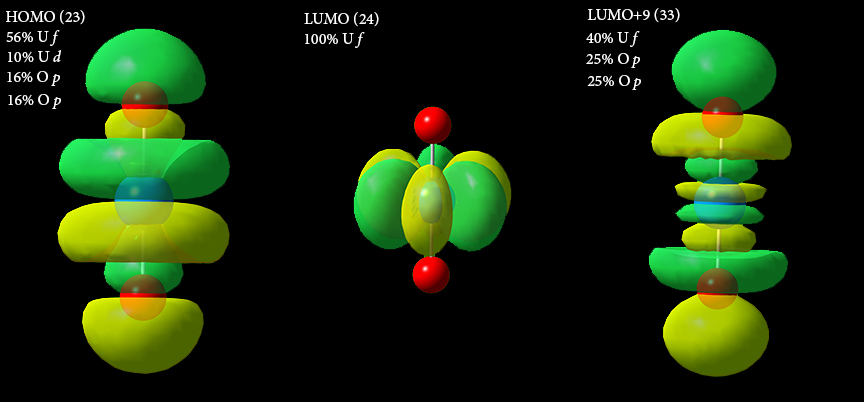
The HOMO is comprised of the 5f and 6p orbitals from the uranium atoms—about 56% and 10% respectively—as well as a p orbital from each oxygen atoms (~16% each). The LUMO is a Uranium f orbital. Orbital 33 (LUMO+9), the antibonding counterpart to the HOMO, is similarly comprised of uranium f (~40%) and oxygen p (~25% each) orbitals.
The HOMO and LUMO+9 pair are typical of the inverse-trans-influence (ITI) phenomenon which stabilizes some linear ligand-metal-ligand bonds (where a cis arrangement would otherwise be favored).
This effect is responsible for the surprising stability of uranyl and other similar compounds.
References:
P. F. Walch and D. E. Ellis. “Effects of secondary ligands on the electronic structure of uranyls,” The Journal of Chemical Physics, 65 (1976) 2387. DOI:10.1063/1.433354
Tatsumi, K. and Hoffmann, R. “Bent Cis d0 MoO22+ vs. Linear Trans d0f0 UO22+: A Significant Role for Nonvalence 6p Orbitals in Uranyl,” Inorg. Chem., 19 (1980) 2656-58. DOI: 10.1021/ic50211a035
P. Pyykkó and L. L. Lohr, Jr. “Relativistically Parameterized Extended Hückel Calculations. 3. Structure and Bonding for Some Compounds of Uranium and Other Heavy Elements,” Inorg. Chem., 20 (1981) 1950-59. DOI: 10.1021/ic50221a002
Recent ITI review: M. Gregson, E. Lu, D. P. Mills, F. Tuna, E.J.L. McInnes, C. Hennig, A.C. Scheinost, J. McMaster, W. Lewis, A.J. Blake, A. Kerridge and S.T. Liddle. “The inverse-trans-influence in tetravalent lanthanide and actinide bis(carbene) complexes,” Nature Communications, 8 (2017) 14137. DOI: 10.1038/ncomms14137
Last updated on: 9 July 2018.































