- Introduction
- G16 Overview
- GV6 Overview
- Excited States
- Performance
- GPUs
- Example
- Ease of Use
Continuing the nearly 40-year tradition of the Gaussian series of electronic structure programs, Gaussian 16 offers new methods and capabilities which allow you to study ever larger molecular systems and additional areas of chemistry. GaussView 6 offers a rich set of building and visualization capabilities. We highlight some of the most important features on this page.
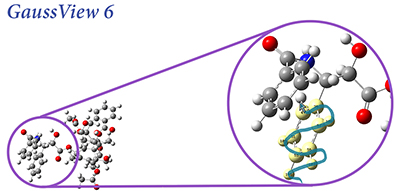
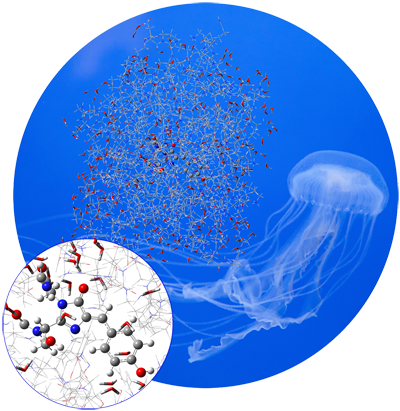
Explore New Substances and Environments: Green Fluorescent Protein
GFP is a protein that fluoresces bright green when exposed to light in the blue-to-ultraviolet range. The chromophore is shown in the inset below. The molecule was first isolated in the jellyfish species Aequorea victoria, which is native to the Pacific northwest coast of North America. Since then, it has been studied extensively, and variants of the molecule with enhanced fluorescence properties have been engineered.
GFP consists of a chromophore within a protein chain composed of 238 amino acids. The isolated chromophore is not fluorescent, so modeling it in its protein environment is essential. GFP’s fluorescence cycle involves an initial excitation to its first excited state, a proton transfer reaction on the S1 potential energy surface, and finally a relaxation back to the ground state.
The following features of Gaussian 16 and GaussView 6 are useful for modeling fluorescence in this compound:
 |
|
- Gaussian can optimize the geometries of the minima and transition structures on the excited state PES with TD-DFT. GaussView includes features for setting up reliable QST2/QST3 transition structure optimizations with minimum effort.
- An IRC calculation in Gaussian can follow the corresponding S1 PES reaction path, which can then be animated in GaussView.
- Gaussian can perform vibrational frequency analysis in order to predict the IR/Raman spectra and normal modes. A variety of other spectra are also available, including vibronic spectra. GaussView can display plots of the predicted spectra and animate the associated normal modes (as applicable).
- GaussView makes it easy to examine the results of one calculation and then set up and initiate the next calculation in sequence via an intuitive interface to all major Gaussian 16 features.
[Thompson14] and [Petrone16] are excellent studies of GFP using the previous version of Gaussian. See chapter 9 of [Foresman15] for a detailed tutorial about preparing PDB files for use with the ONIOM facility in Gaussian.
Overview of What’s New in Gaussian 16
Gaussian 16 brings a variety of new methods, property predictions and performance enhancements. Details about many of them are given elsewhere in this brochure.
Modeling Excited States
- Analytic frequency calculations for the time-dependent (TD) Hartree-Fock and DFT methods, including ONIOM electronic embedding fully coupled with the environment of the MM region, without additional approximations [WilliamsYoung17p].
- Geometry optimizations with the high accuracy EOM-CCSD method (analytic gradients) [Caricato12a].
- Anharmonic analysis for calculating IR, Raman, VCD and ROA spectra [Bloino12, Bloino12a, Bloino15]. Calculations in solution take the interaction between the excitation and the solvent field fully into account [Cappelli11].
- Vibronic spectra prediction [Barone09, Bloino10, Baiardi13].
- Chiral spectroscopies: electronic circular dichroism (ECD) and circularly polarized luminiscence (CPL) [Barone12, Barone14].
- Modeling of resonance Raman spectroscopy [Egidi14, Baiardi14].
- Computation of electronic energy transfer (EET) [Iozzi04].
- Ciofini’s excited state charge transfer diagnostic (DCT) [LeBahers11, Adamo15].
- EOM-CCSD solvation interaction models of Caricato [Caricato12b].
New Methods
- Many DFT functionals have been added to Gaussian since the initial release of G09, including APFD [Austin12], functionals from the Truhlar group (most recently MN15 and MN15L [Yu16]) and PW6B95 & PW6B95D3 [Zhao05a].
- Additional double-hybrid methods: DSDPBEP86 [Kozuch11], PBE0DH, PBEQIDH [Bremond11,Bremond14].
- Empirical dispersion for a variety of functionals, using the schemes of Grimme (GD2, GD3, GD3BJ) [Grimme06, Grimme10, Grimme11] and others.
- The PM7 semi-empirical method, both in the original formulation [Stewart13], and with modifications for continuous potential energy surfaces [Throssel17p].
Performance Enhancements
- Support for NVIDIA K40 and K80 GPUs on Linux systems, for HF and DFT calculations.
- Enhanced parallel performance on larger numbers of processors.
- Speedups for key parts of several calculation types.
- CASSCF improvements and support for active spaces of up to 16 orbitals [Li11].
Ease of Use Features
- Automatically recalculate the force constants every nth step of a geometry optimization.
- An expanded set of Link 0 commands and corresponding Default.Route file directives.
- Tools for interfacing Gaussian with external programs in compiled languages such as Fortran and C and/or in interpreted languages such as Python and Perl.
- Generalized internal coordinates: define arbitrary redundant internal coordinates and coordinate expressions for use as geometry optimization constraints.
Overview of What’s New in GaussView 6
GaussView 6 provides support for all major Gaussian 16 features as well as offering additional modeling capabilities of its own.
Building and Manipulating Molecular Structures
- Select step(s) to open from multi-job Gaussian input files.
- New advanced open dialog, allowing options to be modified and retained across sessions: whether to load intermediate geometries, weak bond inclusion, PDB file processing options, and similar settings.
- New brush selection mode to accurately choose atoms within dense regions.
- Open PDB files created by Amber.
- Reduce symmetry of a molecule to a specified point group (using the same feature as for increasing and constraining symmetry).
- Specify custom bonding parameters.
Gaussian Job Setup & Execution
- Support for new features in Gaussian 16 and updates to existing job setup options.
- Create and/or initiate identical calculations for a series of molecules in a single step.
- Create new Gaussian input files which use the molecule specification and other data from a checkpoint file.
- Support for a wide range of Link 0 commands.
- Expanded access to population analysis options.
- Preview the input file as it is created.
- The SC Job Manager provides a straightforward, customizable queueing system for the local computer.
Additional Modeling Capabilities
- Perform conformational searches using the GMMX add-on package. GaussView allows you to:
- Specify the force field, energy range and other parameters for the search.
- Open some or all of the identified conformations into a molecule group.
- View an energy plot for the set of conformations.
- Set up follow-up calculations for desired conformations in a single step.
- Optional full AMPAC interface integration.
Examine & Visualize Results
- Select step(s) to open from multi-calculation Gaussian results files.
- Visualize predicted bond lengths and bond orders.
- Results from anharmonic frequency calculations can be plotted alone or in combination with the harmonic results.
- Include multiple calculation results in the same plot. Spectra from multiple conformations can be Boltzmann-averaged.
- Customize plots: specify line colors and widths, canvas and background colors, label and title fonts, X- and Y-axis settings, and so on.
- Display the solvation cavity surface for an SCRF calculation.
- Plot the results of Optical Rotary Dispersion (ORD) calculations.
- Scale frequencies by a specified value for plotting.
- Support for Gaussian trajectory calculations.
- Image capture enhancements: background color, save images of multiple molecules in a single operation.
- Image capture and printing defaults.
- Enhanced movie creation: support for MPEG4 files; set options for frame looping and time delays.
File Conversion & Customization
- Convert files between different formats; AMPAC input files, Gaussian input files, MDL Mol and SDF files, GMMX input files and Sybyl Mol2 files.
- Set defaults for image capture, movie generation and custom bonding parameters.
- Context-specific help system.
Sophisticated Modeling of Excited States
Excited state methods and properties received a lot of attention as we developed Gaussian 16. With its analytic TD-DFT frequencies, you can optimize excited state transition structures and perform IRC calculations. Analytic EOM-CCSD gradients let you optimize the structures of molecules that require a high accuracy excited state treatment.
Anharmonic Vibrational Analysis
Standard vibrational frequency analysis employs the double harmonic approximation, the simplest description of the vibrations and the molecule’s interaction with the electromagnetic field of the incident photons. It treats nuclear vibrations as simple harmonic motion about the minimum energy structure and uses a correspondingly simplified model for the electromagnetic field interaction. For many systems, this is sufficient, but sometimes the approximation reduces the accuracy of the predicted spectra.
Anharmonic frequency analysis relaxes both parts of the double harmonic approximation by introducing additional mathematical terms: higher derivatives of the energy, dipole moment, polarizability (as appropriate to the type of spectroscopy being modeled). Doing so results in changes in the locations of the fundamental frequencies and enables the prediction of overtone and combination bands. Later revisions of Gaussian 09 included anharmonic IR and Raman spectra, and Gaussian 16 adds anharmonic VCD and ROA spectra.
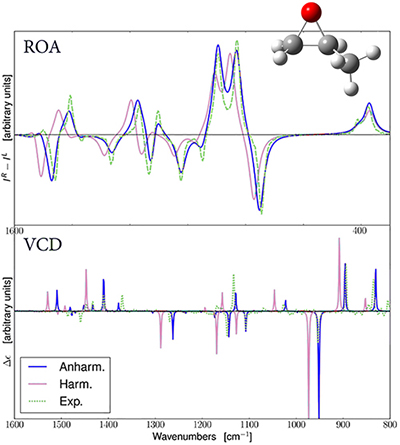
Predicted ROA and VCD Spectra for R-Methyloxirane
The spectra predicted with harmonic and anharmonic analyses are in pink and blue (respectively). The experimental spectra are in green [Merten13], and they have been added to the GaussView plot. For both ROA and VCD, the anharmonic results are in better agreement with the observed spectrum [Bloino15].
Resonance Raman Spectroscopy
Gaussian 16 can predict Resonance Raman (RR) spectra. RR spectroscopy is a type of Raman spectroscopy where the incident laser frequency is close in energy to an electronic transition of the compound being studied. This has the advantage of enhancing the intensity of the scattered light.
These experiments typically scan over a range of frequencies for the incident light. The resulting data can be plotted as a three dimensional surface: the incident light frequencies and the corresponding observed peaks are plotted in the X-Y plane, with the intensity determining the height of the curve above the plane.
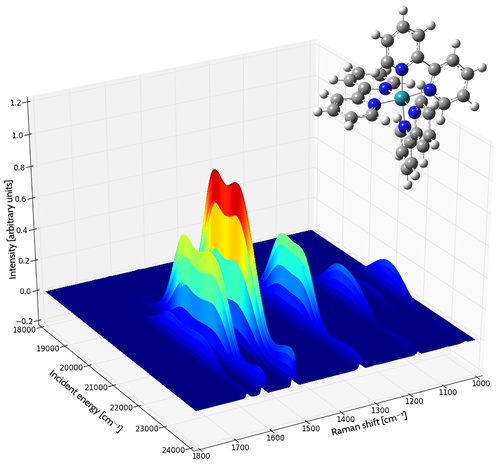
Resonance Raman Spectrum of the tris(2,2’-bipyridyl)-ruthenium(II) Complex
Each curve shows the intensity of the Raman shift produced by various frequencies of incident light. The area under each curve is filled, colored by the magnitude of the intensity (blue to red as the intensity increases). The spectrum was computed in acetonitrile solution [Baiardi14].
Franck-Condon/Herzberg-Teller Analysis and Vibronic Spectra
Gaussian 16 can compute vibronically-resolved electronic spectroscopy for one photon absorption processes. In a vertical excitation resulting from the absorption of a photon, a molecule moves from its ground electronic state to an excited state. The geometry of the excited state immediately afterwards is not the equilibrium structure of the excited state, i.e., the minimum on the excited state potential energy surface. Rather, because the time scale in which electronic transitions occur is so small compared to nuclear motions, the nuclei are nearly unaffected, and the ground state equilibrium geometry is initially retained.
 |
A consequence of the geometry of the excited state being initially unchanged from the ground state is that the vibrational state taken on by the molecule in its excited state need not be the lowest one. Rather, when the molecule transitions to the excited state, it moves to a vibrational state that is instantaneously compatible with its current one. In reality, the actual energy transition observed in an experiment is a series of many energy transitions from the various vibrational levels of the ground state to the various vibrational levels of the excited state, with the strength of each individual transition depending on the population of that state and the overlap between the ground and excited vibrational wavefunctions for that transition. These effects are the basis of the Franck-Condon principle. Gaussian 09 introduced Franck-Condon and Herzberg-Teller analysis capabilities (as well as their combination), allowing these spectra to be predicted. Gaussian 16 significantly enhances these features, adding the ability to predict intensities, perform band assignment and providing other data about overlap between states. |
Below are examples of the results of Gaussian 16’s vibronic analysis capabilities as visualized in GaussView 6:
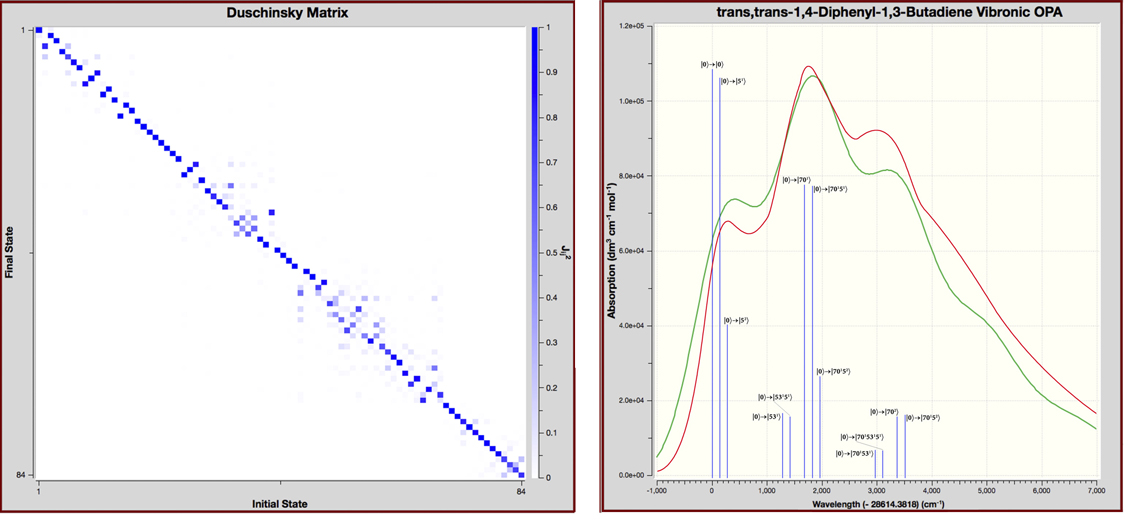
Duschinsky Matrix and Vibronic One Photon Absorption Spectrum for trans,trans-1,4-Diphenyl-1,3-Butadiene
The Duschinsky matrix (left) is a visual depiction of vibrational mode overlaps between the corresponding modes in the ground state and the excited state. It is a good approximation of this data so long as no large distortion occurs during the transition. In these plots, mode numbers for the ground state run along the X-axis, and those for the excited state run down the Y-axis. The intensities of the squares in the plot range from solid (100% state overlap) to about eight tone (~12% overlap). This example shows mostly strong overlap along the diagonal indicating that the Franck-Condon perturbation is a good approach to describing the vibronic coupling. Further, modes with significant differences can readily be identified.
The plot on the right shows the predicted (red) and experimental (blue) vibronic spectrum for the same compound [Foresman15]. The transitions requested in the calculation are represented by the vertical green lines which we have labeled with their specific transition. We added the observed spectrum and transition labels to the GaussView display. Note that transitions can be computed for only a portion of the total spectrum if desired. The X-axis indicates the energy relative to the 0-0 transition (a GaussView plot option).
Performance Enhancements
Parallel Calculations on Larger Numbers of Processors
Gaussian 16 performs significantly better than previous versions when run across more than 10-20 cores. An APFD/6-31G(d) Opt=CalcFC Freq calculation on Alanine 25 is 1.8 times faster in Gaussian 16 than in Gaussian 09 (see graph on the left below). The CalcFC and Freq portions of the calculation comprise 47% of the execution time in Gaussian 16 compared to 61% in Gaussian 09.
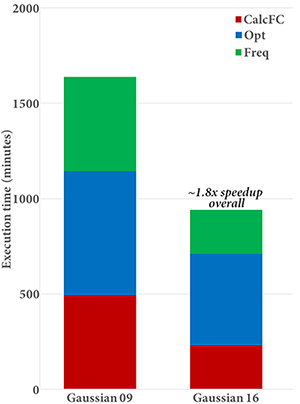 |
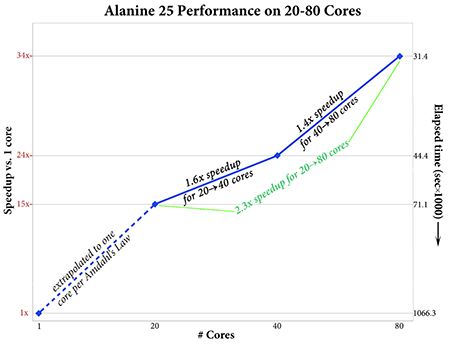 |
Gaussian 16’s performance scales effectively to 80 cores or more (depending on the calculation and molecule). The plot on the right above gives the speedups for 20, 40 and 80 cores for an APFD/6-31G(d) Freq calculation on Alanine 25. This job shows good parallel speedups with increasing numbers of processors; the speedup when moving from 20 to 80 cores is about 2.3, and the estimated speedup for 80 cores over a single processor is 34.
Algorithmic Improvements
Gaussian 16 also offers a wide variety of other performance improvements to many different parts of the program. Among the most significant are the following:
- An optimized memory algorithm which avoids I/O during CCSD iterations.
- Enhancements to GEDIIS optimization feature providing increased stability and more sophisticated automated detection/selection of the appropriate algorithm [Frisch17p].
- CASSCF improvements allowing active spaces of up to (16,16) to be used [Li11].
- Much faster performance for the low level part of the EPT (OVGF) compound model for predicting photoelectron spectra [DiazTinoco16].
Running Calculations on GPUs with Gaussian 16
As a result of a fruitful, ongoing collaboration between Gaussian Inc., NVIDIA and Hewlett-Packard Enterprise, Gaussian 16 supports running calculations using NVIDIA GPUs. NVIDIA Tesla K40, Tesla K80, Tesla P100, Tesla V100 and A100 GPUs can be used in Hartree-Fock and DFT calculations, including energies, optimizations and frequencies, for ground and excited states (TD), and for closed shell and open shell molecules. ONIOM, SCRF solvation and all major properties are supported, as are all DFT functionals available in Gaussian 16, making the most frequently-run Gaussian calculations applicable to execution with GPUs.

NVIDIA A100 GPUs use the NVIDIA Ampere GPU architecture to achieve ~9.7 TFlops peak performance (double precision), and have 40GB HBM2 or 80GB HBM2e memory.
NVIDIA Tesla V100 GPUs (illustrated above) use the NVIDIA Volta GPU architecture to achieve ~7.8 (SXM2) or ~7 (PCIe) TFlops peak performance (double precision), and have 16GB-32GB HBM2 memory.
NVIDIA Tesla P100 GPUs use the NVIDIA Pascal GPU architecture to achieve ~5 TFlops peak performance (double precision), and have 12-16GB HBM2 memory.
NVIDIA Tesla K40 & Tesla K80 GPUs have 12GB 5GHz GDDR5 VRAM and achieve peak performance of ~1.5 TFlops (double precision), with 1 and 2 GPUs per board (respectively).
Performance Results for Example Calculations
The following table provides some example performance data for the current version of Nvidia V100 GPU support. The timings compare running a calculation across 28 CPU cores on a DGX-1 server (Broadwell CPUs) versus running on the same server across 28 CPU cores and 8 GPUs (with 8 CPU cores serving as GPU controllers during the GPU-enabled parts of the calculation).

GPU Parallelization Strategy
Within Gaussian 16, GPUs are used for a small fraction of code that consumes a large fraction of the execution time. The implementation of GPU parallelism conforms to Gaussian’s general parallelization strategy. Its main tenets are to avoid changing the underlying source code and to avoid modifications which negatively affect CPU performance. For these reasons, OpenACC was used for GPU parallelization.
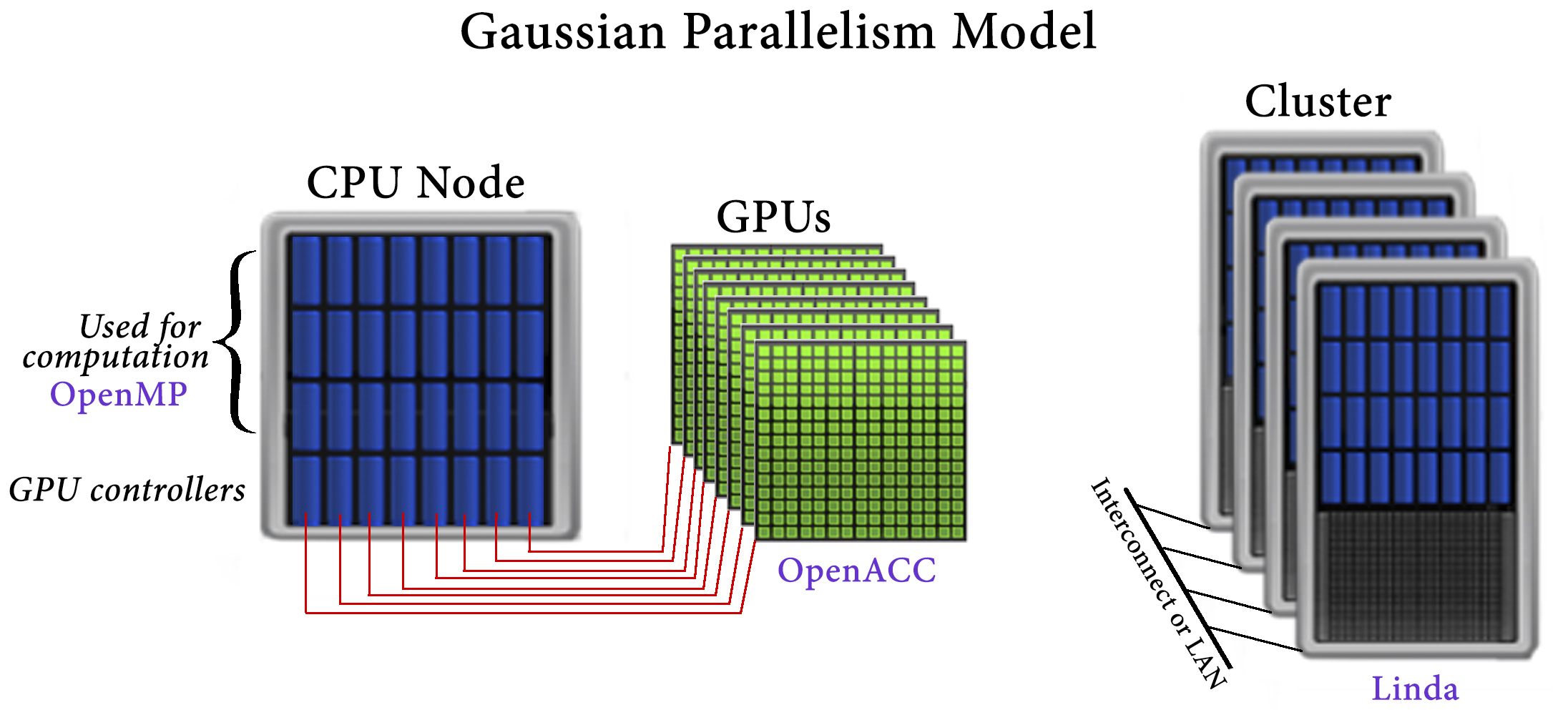
The Gaussian approach to parallelization relies on environment-specific parallelization frameworks and tools: OpenMP for shared-memory, Linda for cluster and network parallelization across discrete nodes, and OpenACC for GPUs.
The process of implementing GPU support involved many different aspects:
- Identifying places where GPUs could be beneficial. These are a subset of areas which are parallelized for other execution contexts because using GPUs requires fine grained parallelism.
- Understanding and optimizing data movement/storage at a high level to maximize GPU efficiency.
- PGI’s sophisticated profiling and performance evaluation tools were vital to the success of the effort.
NVIDIA HPC SDK: Compilers with OpenACC
The compilers included in the NVIDIA HPC SDK fully support the current OpenACC standard as well as important extensions to it. NVIDIA is a key contributor to the ongoing development of OpenACC.
OpenACC enables developers to implement GPU parallelism by adding compiler directives to their source code, often eliminating the need for rewriting or restructuring. For example, the following Fortran compiler directive identifies a loop which the compiler should parallelize:
!$acc parallel loop
Other directives allocate GPU memory, copy data to/from GPUs, specify data to remain on the GPU, combine or split loops and other code sections, and generally provide hints for optimal work distribution management, and more.
The OpenACC project is very active, and the specifications and tools are changing fairly rapidly. This has been true throughout the lifetime of this project. Indeed, one of its major challenges has been using OpenACC in the midst of its development. The talented people at PGI, now part of NVIDIA, were instrumental in addressing issues that arose in one of the very first uses of OpenACC for a large commercial software package.
Project Contributors
 |
 |
 |
 |
 |
Roberto Gomperts |
Michael Frisch |
Kyle Jacobs |
Brent Leback |
Giovanni Scalmani |
| NVIDIA | Gaussian | NVIDIA | NVIDIA/PGI | Gaussian |
Application Example: ROA Spectrum of Aeroplysinin-1
Aeroplysinin-1 is a brominated compound that is of interest as an antiangiogenic drug [NietoOrtega11]. Here we will briefly discuss how Gaussian and GaussView can be used to predict its ROA spectrum in order to determine the molecule’s absolute configuration.
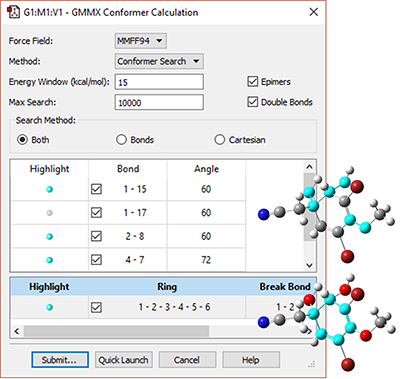 |
This molecule has many possible conformations, and predicting its ROA spectrum will need to take into account all of the energetically important ones. The GMMX add-on to GaussView performs efficient and comprehensive conformational searches. We use the dialog at the left to specify the parameters of the search procedure, including the force field (here MMFF94), the types and specific bonds and rings to modify and the energy range into which potential structures must fall (<15 kcal/mol of the lowest energy structure). |
| The conformational search finds 25 unique structures within the specified energy range. The structures can be opened into a single molecule group in one step, and the Energy plot feature graphs their relative energies. After examining the structures, we run modest accuracy optimizations to determine the set of unique conformations, which we then optimize and perform a vibrational frequency analysis with a high accuracy model chemistry. | 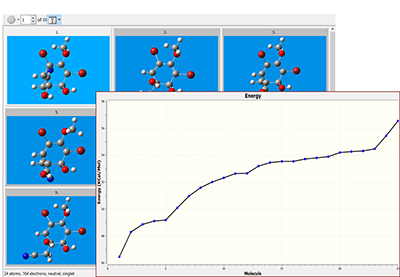 |
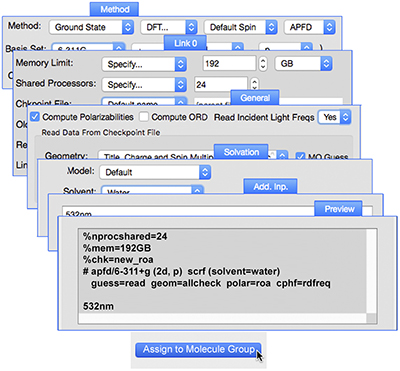 |
GaussView can set up identical jobs for all of the structures within a molecule group at the same time (using the Assign to Molecule Group button). The illustration shows the various controls we used to set up the final series of jobs: ROA spectra predictions starting from the results of the high accuracy optimization plus frequency calculation for the six conformations that conribute at least 5% to the Boltzmann distribution. The new Preview panel in the Gaussian Calculation Setup dialog displays the input file generated from the dialog selections. |
|
Once the Gaussian calculations have been set up, we can run them from within GaussView. The SC Job Manager facility provides a queueing system for the local computer, and we can save all the input files and submit them for execution as a group. The dialog at the left shows the multiple file save facility. We use it to assign unique file names to the input file for each structure in the molecule group, and then save all of them in a single operation. |
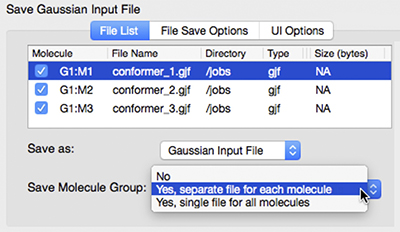 |
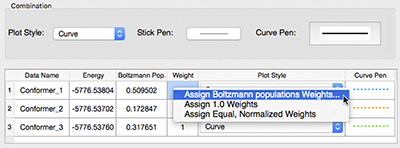 |
Once the ROA calculations have completed, we can examine the predicted spectra of each conformation individually or via a multistructure spectrum plot (pictured below). The dialog shown at the right allows you to customize the plot by specifying the various line colors, types and widths. You can also scale the various curves with their Boltzmann weights as well as including the conformationally averaged combination curve. |

Predicted and Observed ROA Spectra
This GaussView plot shows the predicted spectra for the three lowest energy conformations of (1R,6R)-Aeroplysinin-1 (the dotted lines), as well as the computationally-averaged spectrum (solid black line), over the range of 900-1700 cm-1. We have added an inset comparing the predicted and observed spectra for both diastereomers of this compound [NietoOrtega11]. The experimental spectrum corresponds to the (1S,6R) form; compare, e.g., the circled area in the predicted (1R,6R) spectrum. See [Foresman15, Exercise 7.8] for more details about this molecule.
Ease of Use Features
Gaussian 16
- Opt(Recalc=n) automatically updates the force constants with accurate analytic values every nth step of a geometry optimization. It is helpful for molecular systems where large structural changes occur during the course of the optimization.
- An expanded set of Link 0 commands: the supported set of directives provides simple, direct management of calculation resource usage. All Link 0 commands have counterparts in Default.Route file directives, so resources can be specified and managed on a system-wide basis. There are also corresponding command line options for all them so that the same features are available to scripts.
- Tools for interfacing Gaussian with other programs, both in compiled languages such as Fortran and C and with interpreted languages such as Python and Perl. These tools are made available under a variation of the Mozilla Public License. They are designed for the following scenarios:
- Scripts which automate running multiple related Gaussian jobs.
- Post processing of Gaussian results.
- Computations in other programs can use intermediate data generated by Gaussian, either by running an independent program that uses previously-calculated Gaussian results or by incorporating results from an external program into Gaussian calculations (e.g., ONIOM calculations in which the energies and forces are calculated using a method not available in Gaussian 16).
- Rapid prototyping of new models/methods by using quantities computed by Gaussian so that only the unique aspects of the new model need to be implemented.
- Classroom exercises employing interpreted languages such as Python or MatLab, so that they can focus on a specific issue without having to provide code for unrelated parts.
- Generalized internal coordinates (GICs): arbitrary redundant internal coordinates can be defined. GICs can potentially be used for freezing various structural parameters during the optimization of a molecular system, specifying parameters over which to perform a scan, and defining constraints for geometry optimizations based on structural parameters or complex relationships between them.
Last updated on: 11 March 2022.